Главное про описательную статистику в теннисе. Ч. 1
Что вообще такое описательная статистика и зачем она нужна? Тот самый случай, когда ответ на вопрос заложен в само название. По своей сути, описательная статистика - это набор статистических показателей, которые характеризуют наш набор данных и позволяют быстро понять с чем мы имеем дело.
Перед погружением в различные виды описательных статистик давайте поговорим о том, какие бывают наборы данных. Что, собственно, мы собираемся исследовать?
Генеральная совокупность и выборка.
В качестве набора данных может выступать как генеральная совокупность, т.е. все имеющиеся в природе данные определенного типа. Например, все матчи ATP, сыгранные в Открытой Эре, или же некоторая выборка - матчи ATP 2023 года. Этот набор матчей текущего года и ляжет в основу нашего сегодняшнего поста: 1 845 игр уровня ATP-тура 2023 года, в формате 3-х сетов.
Во многих областях, в том числе и в спортивной статистике, порой непросто найти данные всей генеральной совокупности и мы зачастую работаем именно с выборками. Канонический пример: добыть информацию о росте всех людей на планете практически невозможно, в то же время вполне реально собрать данные о росте 1 000 - 2 000 людей каждого из континентов. С высокой долей вероятности, эта выборка будет репрезентативна и даст понимание о статистических закономерностях роста людей на Земле.
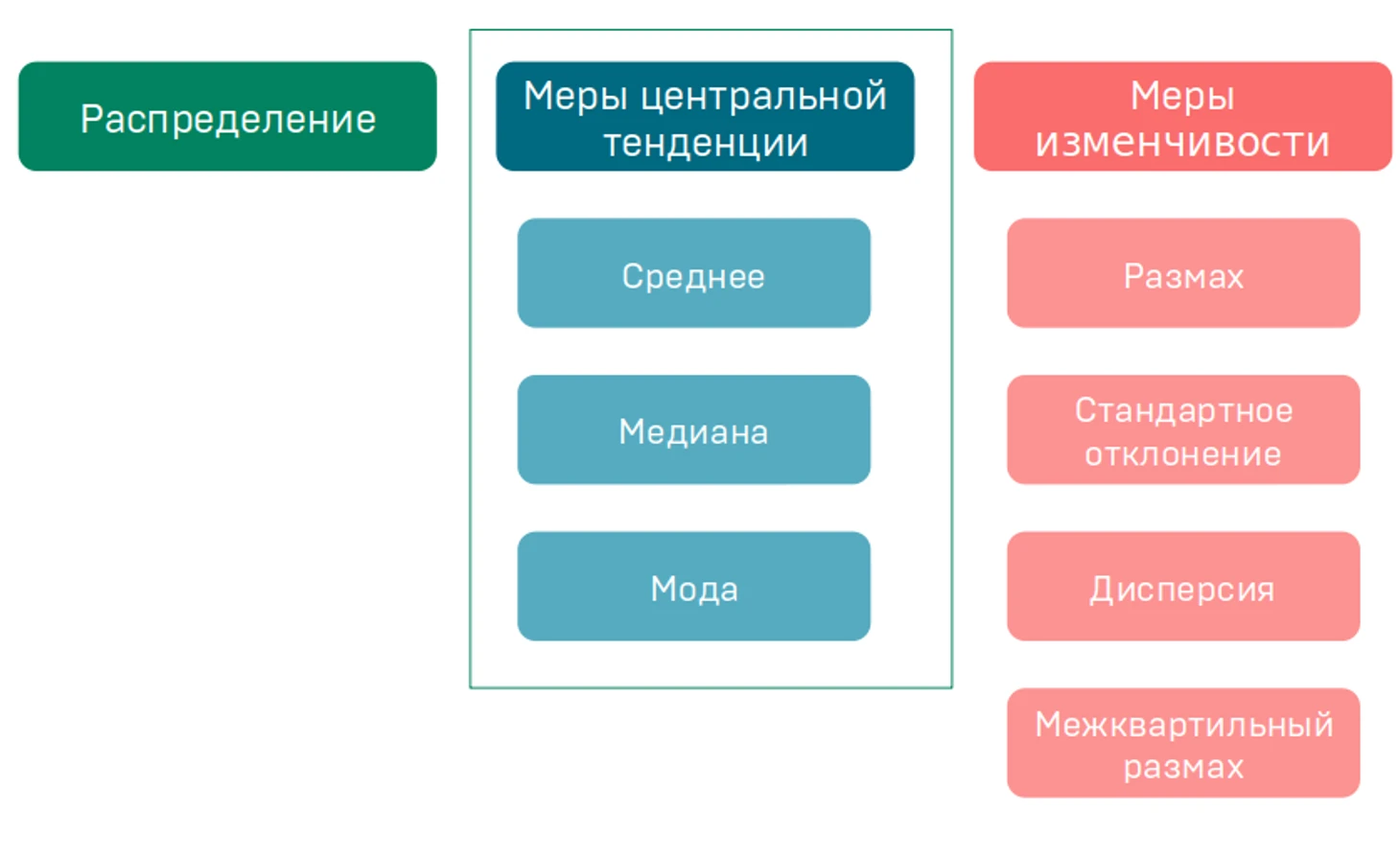
Описательные статистики
Вернемся к нашей теме. Описательные статистики принято разделять на три категории: распределение, меры центральной тенденции, меры изменчивости.
Сегодня речь пойдет об одной из мер центральной тенденции - среднем.
Среднее.
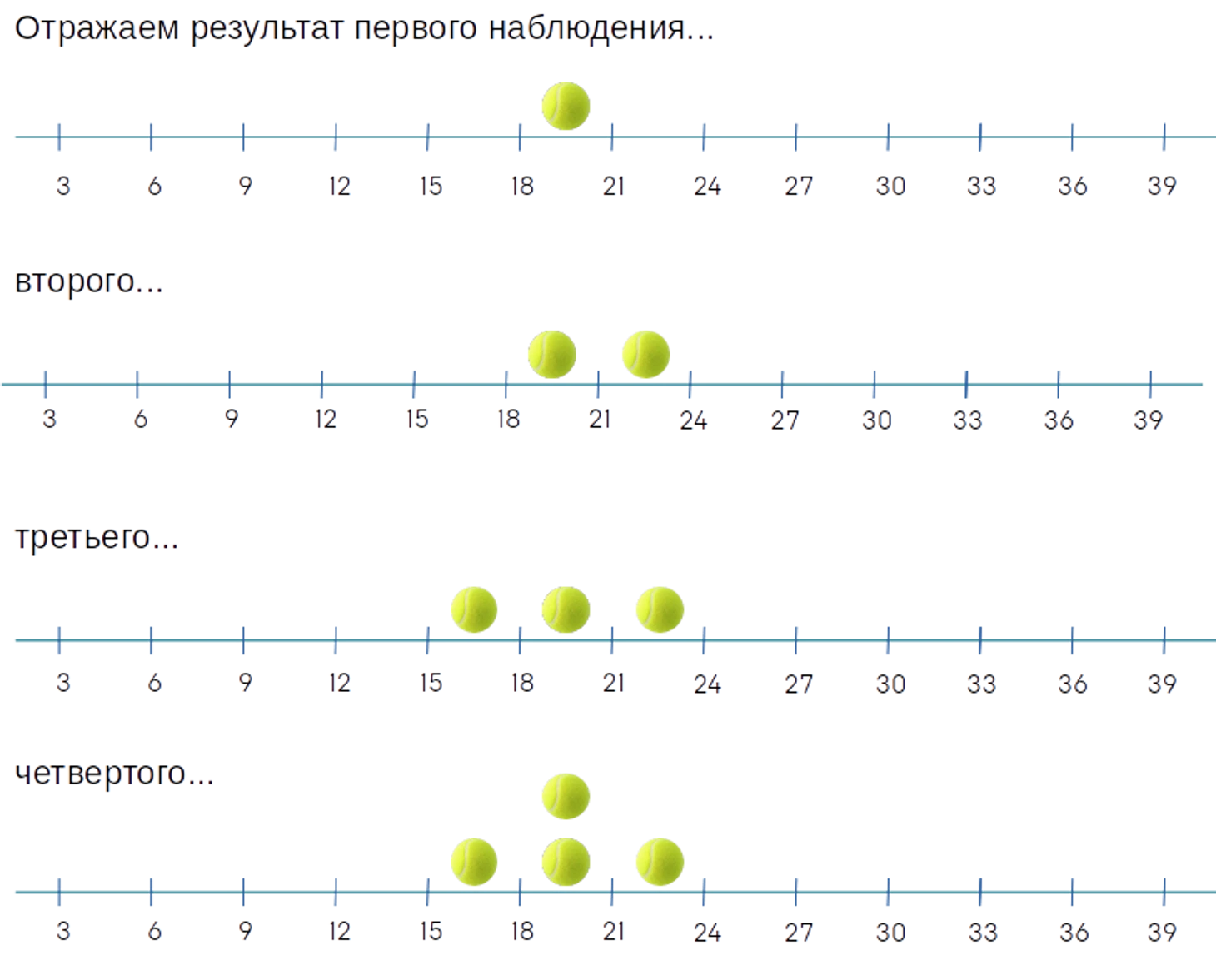
Как по мне, наиболее удачный параметр нашего набора, который поможет разобраться со средним и другими мерами центральной тенденции - это количество геймов в матче.
Вспоминаем гистограммы...
Построим шкалу от 0 [минимальное число геймов, если кто-то снялся прямо в начале игры] до 39 геймов [максимально возможное число геймов]
Разобьем шкалу на промежутки кратные трем (0-3 гейма, 3-6 геймов, 6-9 геймов и т.д.) для наглядности отображения наших данных.
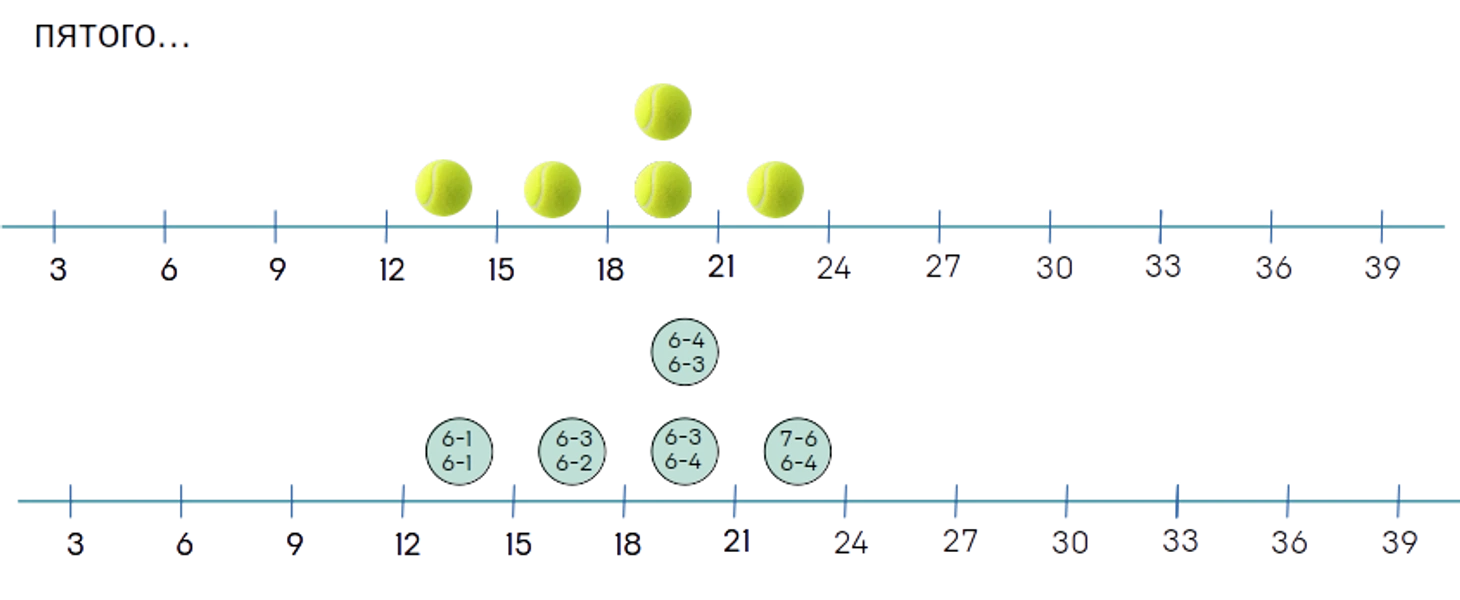
Думаю, что вполне достаточно, для того чтобы поговорить об основных видах среднего: среднем арифметическом, среднем взвешенном, среднем геометрическом.
Среднее арифметическое.
Самый простой и широко используемый вид среднего: сумма всех наблюдений делится на количество наблюдений.
В нашем с вами примере у нас есть 5 матчей [наблюдений] со следующим количеством геймов:
14 (6-1 6-1)
17 (6-3 6-2)
19 (6-4 6-3)
19 (6-3 6-4)
23 (7-6 6-4)
Таким образом, среднее арифметическое в нашем случае:
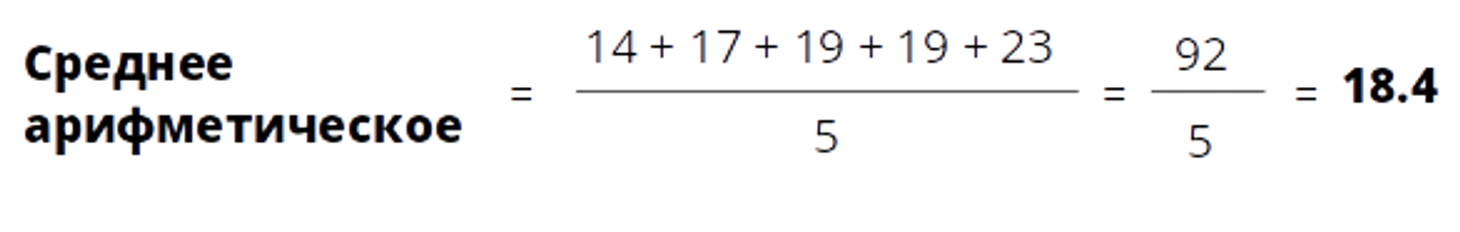
Среднее взвешенное.
Среднее взвешенное - общее название группы разновидностей среднего значения. Да-да, именно общее. Например, среднее арифметическое - не более чем его частный случай, характеризующийся тем, что веса всех наблюдений равны. Давайте разбираться.
Из названия очевидно, что при расчете среднего взвешенного мы каждый элемент выборки взвешиваем, т.е. присваиваем ему какой-то вес [коэффициент], указывающий на его важность в сравнении с другими.
В нашем случае все элементы равны по своей важности для анализа, а значит и их веса имеют одинаковое значение - 1. В то же время, если же мы встретили элемент дважды (19 геймов было в 2 матчах выборки), то формально его коэффициент меняется на 2, но это не более чем характеристика частоты появления элемента в выборке, которая не повлияет на итоговый результат, проверим:
14 - встречается 1 раз
17 - встречается 1 раз
19 - встречается 2 раза
23 - встречается 1 раз
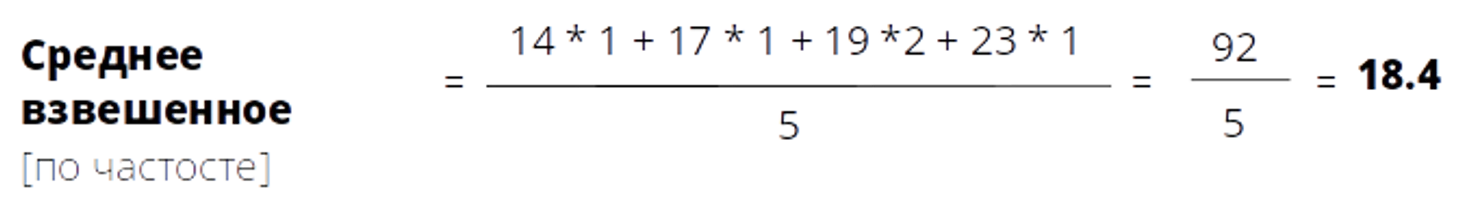
Если же мы, по какой-то причине придаем матчам, в которых было сыграно более 20 геймов, больший вес, например, 1.5, то среднее арифметическое перестанет быть равным среднему взвешенному.
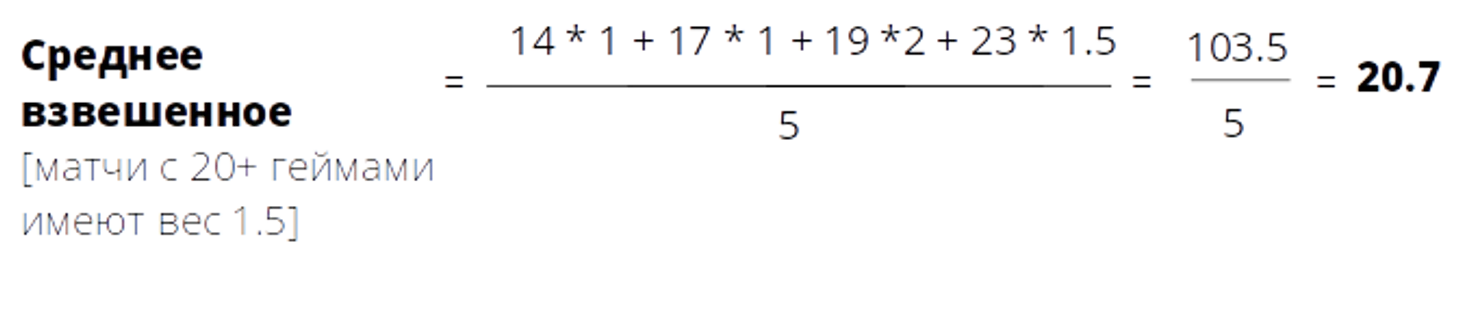
Среднее геометрическое.
Среднее геометрическое используется для расчета средних темпов роста. Проще всего понять на примере.
Представим себе карьеру среднего, но постоянно прогрессирующего игрока ATP-тура:
в первый год своей карьеры в туре он выиграл 5 матчей
во второй год на 20% больше, т.е. 6 игр
на третий уже 9 побед, т.е. на 50% больше, чем годом ранее
в конце концов, на четвертый год игроку удалось одержать победы в 18 встречах, т.е. превысить показатель прошлого года в 2 раза
Именно в таких случаях уместно использовать среднее геометрическое, когда мы хотим определить каков же был средний рост результатов игрока за несколько лет.
Чтобы высчитать среднее арифметическое необходимо перемножить значения прироста (в нашем случае 20% или 1.2, 50% или 1.5 и 100% или 2), а затем из полученного результата извлечь корень, степень которого равняется их количеству, в нашем случае 3.

В порядке информации. Куда менее используемым видом среднего является среднее гармоническое. В виду того, что используется оно чаще всего в финансах или для расчета средней скорости движения, мы не будем подробно останавливаться на его расчетах, вы без труда найдете их на просторах интернета.
Среднее число геймов в матчах ATP тура в 2023 году
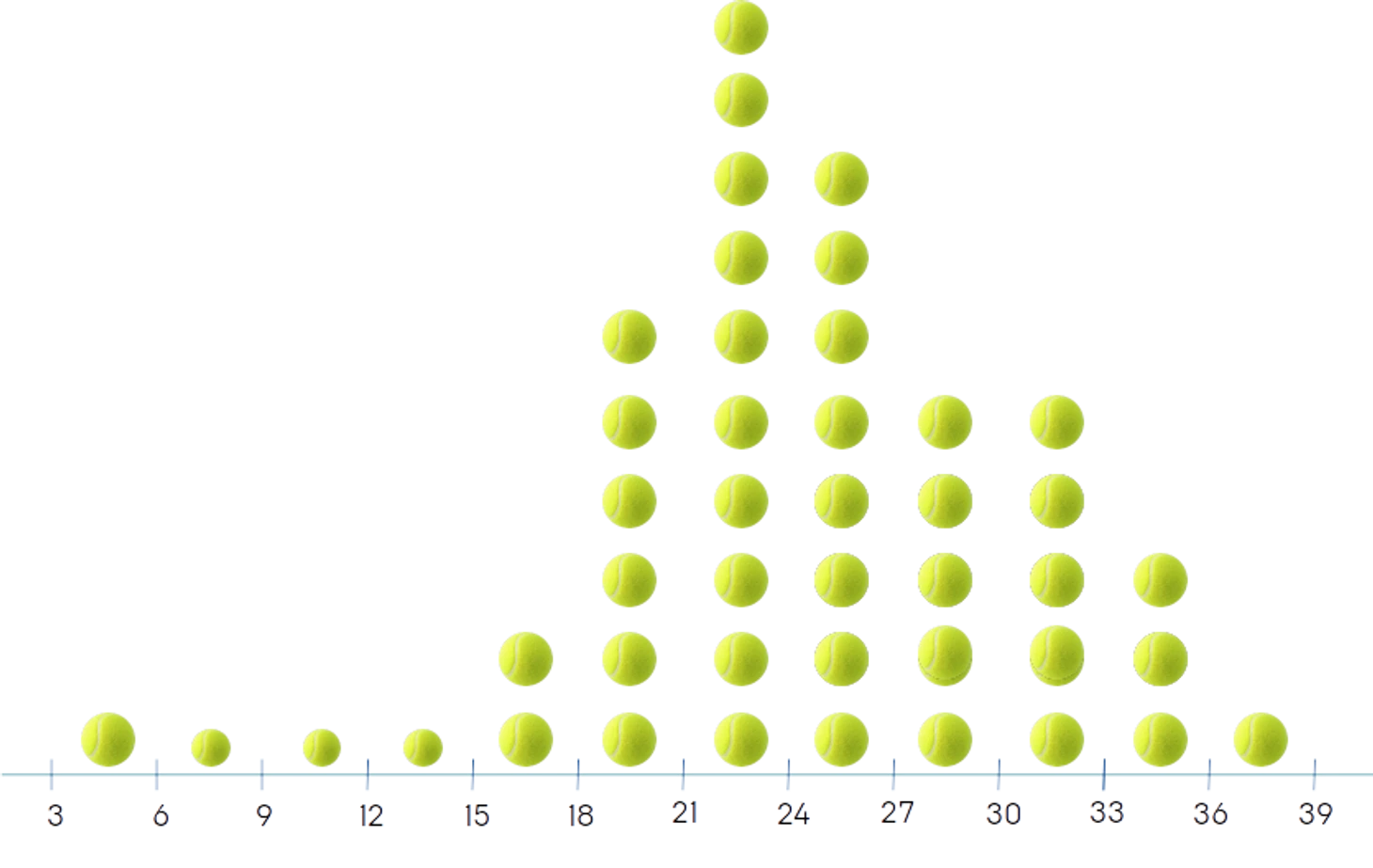
Вернемся к началу и занесем оставшиеся наблюдения. Примерно так, в схематичном виде, будет выглядеть наша гистограмма числа геймов, сыгранных в матчах тура в этом году.
А так будет выглядеть реальная гистограмма распределения.
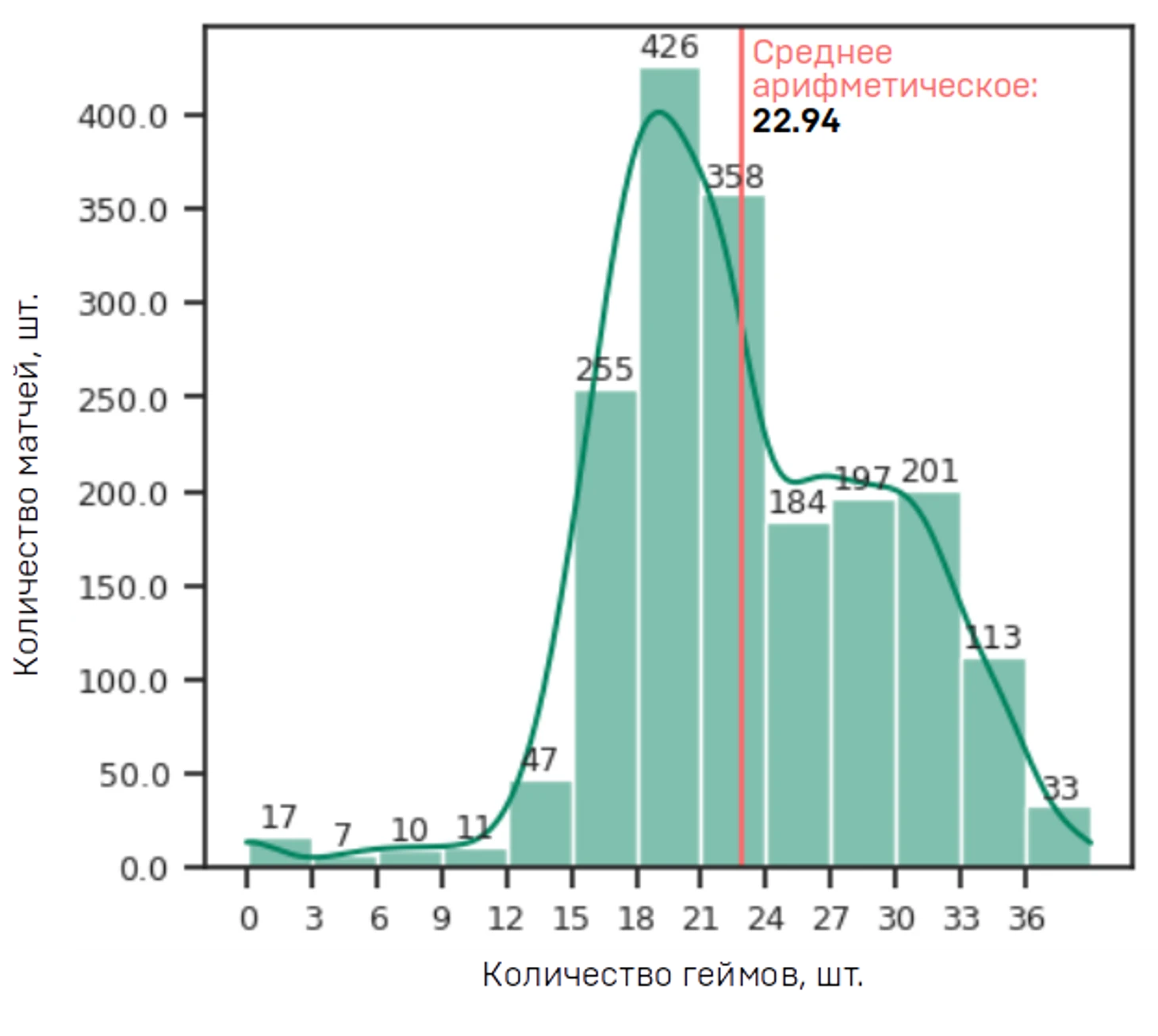
Как вы видите среднее нашей выборки из 5 матчей отличается от среднего по всему числу наблюдений (18.4 против 22.9). Так случилось, что в нашу очень малую выборку попали значения чуть ниже средних. Это абсолютно нормально, с каждым новым внесенным наблюдением, мы бы получали все более и более точные результаты, близкие к реальному значению среднего - 22.94.
Вот мы разобрались с одним из базовых покзаателей статистики - средним, дальше еще интересней! Подписывайтесь и плюсуйте под постом.
И помните, что в спорте играть надо головой. До новых встреч!








