Математик построил модель расчета лучшего пилота «Ф-1» в истории. Шумахер оказался только пятым, Хэмилтон – шестым, Сенна – еще ниже
Внезапный поворот в споре за титул величайшего.
Льюис Хэмилтон повторил рекорд Михаэля Шумахера по победам на Гран-при Айфеля – теперь у них по 91 первому месту. Больше в истории «Ф-1» выиграть не удавалось никому – более того, даже не каждый многократный чемпион мира проезжал столько гонок.
Но можно ли теперь сказать, будто Хэмилтон стал величайшим пилотом? И можно ли считать величайшим самого Шумахера? Похоже, не факт: журнал The Economist вооружился математической моделью доктора математических наук Эндрю Белла из Университета Шеффилда (специализация – продвинутые количественные методы анализа), подробно описанной в научном журнале Количественных методов в спорте за июнь 2016-го, и рассчитал лучших пилотов в истории, отделив их личный вклад от помощи с точки зрения машины, инженеров и везения.
Белл четыре года назад представил весьма сложную математическую модель определения уровня пилота: за основу взяли очковую систему из 1991-2002 годов (10 баллов за первое место в Гран-при, 6 – за второе, 4 – за третье, 3 – за четвертое, 2 – за пятое, 1 – за шестое), а затем рассчитывали вклад пилота, сопоставляя уровни машин соперника в сезоне, выступления напарников и их предыдущие результаты.
В итоге их исследования всех сезонов «Ф-1» вышла вот такая таблица.
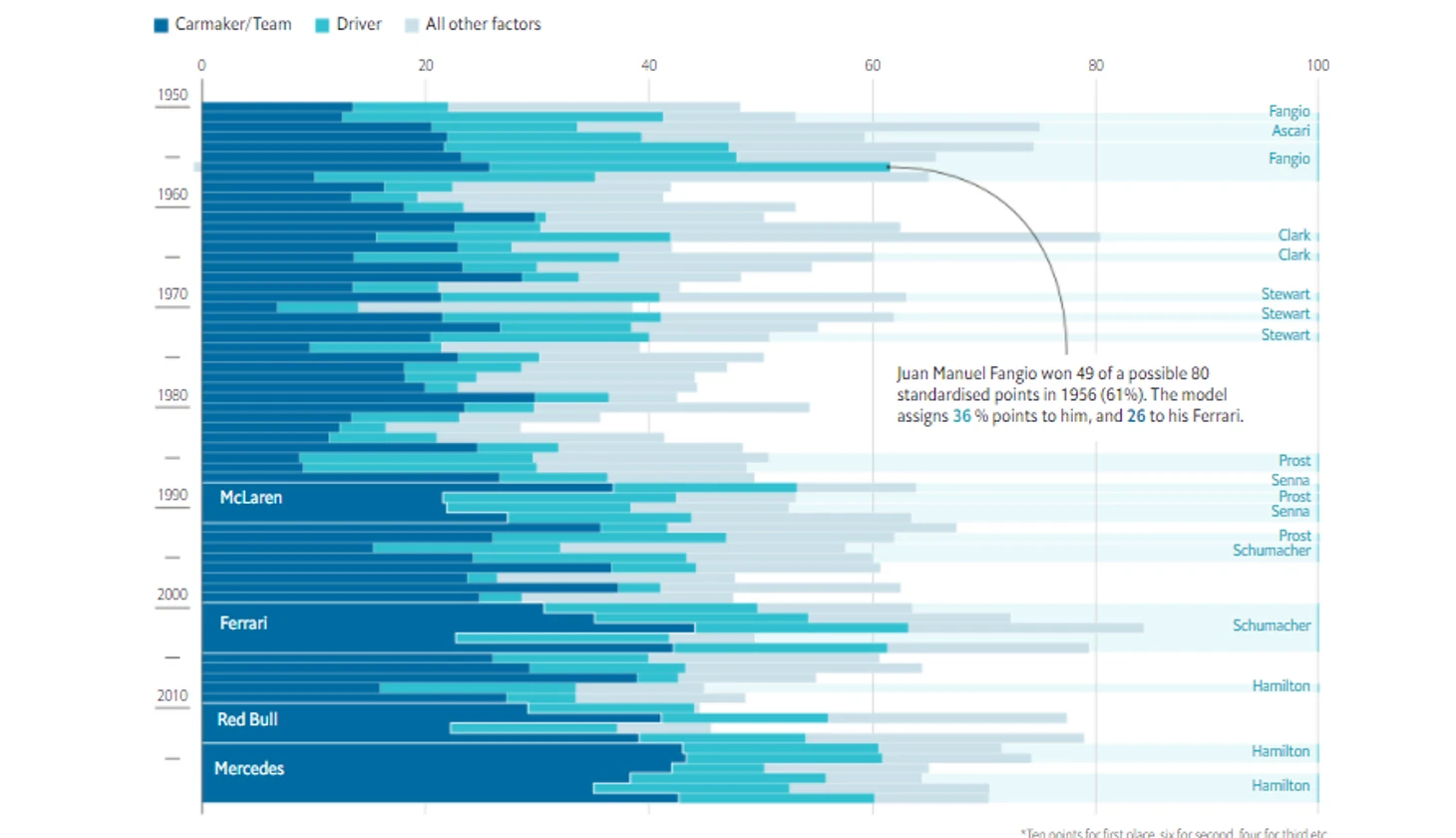
Темно-синие зоны – вклад машины в титул относительно набранных очков, светло-синие зоны – вклад пилота, серые зоны – прочие факторы (вроде везения или аварий соперников).
Расчеты показали: больше всего вклада болида – в победах Михаэля Шумахера в начале 2000-х и у Льюиса Хэмилтона в «Мерседесе» (что интересно, вклад команды в титуле Росберга меньше – но и усилия самого Нико система тоже оценила ниже).
Также большие вклады команды обнаружились и у Айртона Сенны, и у побед «Уильямса» в 90-х, и у титула Фернандо Алонсо в 2006-м, и у Алена Проста в 1985-м, а также у Дэнни Халма в 67-м (спасибо «Брэбэму») и Грэма Хилла в 62-м (спасибо «БРМ»).
Самый «самовозный» титул с наименьшим вкладом пилота – внезапно все та же победа Хилла в 62-м. С ней может посоперничать только титул Марио Андретти и «Лотуса» в 78-м, а также победа Кеке Росберга в 82-м. Также система весьма невысоко оценила вклад Мики Хаккинена в оба чемпионства, а также старания Дэймона Хилла и Жака Вильнева.
Грэм Хилл
За последние 20 лет самым «самовозным», как ни странно, оказался титул Фернандо Алонсо 2006-го – даже сейчас вклады Хэмилтона каждый раз выше (как и старания Феттеля в начале 2010-х).
Наибольший вклад в истории обнаружился у Хуана-Мануэля Фанхио в 1956-м. С его трудами сравнимы только старания Джеки Стюарта, Джима Кларка, Алена Проста и Нельсона Пике.
С другой стороны, в современных титулах за последние 20 лет в победах Шумахера – большой процент и его собственного труда. Сравнимо с ним старались только Дженсон Баттон и Себастьян Феттель.
Но кто же – самый-самый?
Все-таки Фанхио – за ним Кларк, после Прост, затем Стюарт, Шумахер, Хэмилтон и Аскари, а только затем Сенна. Вечный вопрос «Ален или Айртон» здесь закрыт весьма неожиданным образом.
Читать таблицу надо так: Хуан-Мануэль выигрывал в среднем почти по 3 очка за гонку у среднего пилота, Джим – чуть больше 2,5 баллов, и так далее. Михаэль проиграл Джеки совсем немного – меньше десятой. А вот Льюис едва уехал от Альберто – его оставание от топ-5 оказалось внезапно немалым.
Конечно, любая математическая модель – несовершенна для сравнения разных гоночных эпох: ведь пилотаж в начале 50-х требовал от парня за рулем совсем других навыков, чем сейчас. Также система не учитывала по-настоящему сильных пилотов без титула вроде Жиля Вильнева или Стирлинга Мосса. Однако немного фундамента для размышлений насчет представлений о величии современных парней по сравнению с легендами прошлого она все-таки дала: часто вклад пилота сейчас ничуть не меньше, чем в 60-е или 70-е, просто вырос уровень техники и повысилась конкуренция.
Источник: The Economist
Фото: Gettyimages.ru/Clive Mason; commons.wikimedia.org/Lothar Spurzem
Насколько такая объективность осмысленна - это другой вопрос)
Дааа... чудеса ента математика😁