Цепи Маркова – еще один способ оценки эффективности действий футболистов на поле. Фундамент метрик xT и Сontribution
Немного исторического контекста
В далеком 1906 году в Англии стартовал 19-ый сезон Футбольной лиги, победителем которого стал Ньюкасл Юнайтед, набрав 51 очко в 38 турах (сегодня уже мало кто помнит, что до 1981 г в чемпионате Англии, как и других лигах, за победу давали 2 очка, а за ничью 1, и 51 очка при определенном раскладе было достаточно, чтобы занять первое место в чемпионате).
В том сезоне Манчестер Юнайтед, четыре года как поменявший свое название с Ньютон Хит, стал восьмым и уже на следующий год взял свой первый чемпионский титул. Ливерпуль же, взявший свой второй титул в предыдущем сезоне, закончил сезон 1906/1907 на 15 месте, обеспечив себе лишь шестиочковый запас от зоны вылета.
В то же время русский математик Андрей Андреевич Марков, работающий в Санкт-Петербургском государственном университете, в одной из своих работ впервые описывает математический законы, которые позволяют прогнозировать развитие определенных типов процессов окружающего нас мира. Позже такие процессы, состоящие из последовательности случайных событий с определенными свойствами, стали называть по имени математика – Цепи Маркова или Марковские процессы.
В течение 20 века теория цепей Маркова находила применение в различных областях науки, таких как физика, биология, генетика, но одним из самых известных на сегодняшний день примеров применения данной теории стал алгоритм ранжирования web-страниц для поисковых запросов - PageRank, разработанный Сергеем Брином и рядом других авторов в 1998 г., который стал фундаментом поисковой системы Google.
Прошло еще немного времени, наступил 21 век, и математическая теория, придуманная более 100 лет назад, удивительным образом нашла еще одно применение, на это раз в индустрии футбола для оценки действий игроков, о чем и будет рассказано в данной статье.
Десять лет назад в 2011 году американская компания StatDNA, занимающаяся сбором футбольных данных и статистическим анализом, выложила в свободный доступ данные о событиях 123 матчей АПЛ сезона 2010/2011 и устроила соревнования, в которых мог принять участие любой желающий, и основной задачей которых было получение каких-либо новых инсайтов относительно специфики футбольного процесса.
Победителем соревнований стала Сара Радд (Sarah Rudd), которая на тот момент была программистом в Microsoft и работала над поисковой системой Bing (которой не удалось стать настолько же популярной как Google), а в свободное от работы время вела блог футбольной аналитики. Сара разработала модель для тактического анализа и оценки индивидуальных атакующих действий игроков на футбольном поле на основе цепей Маркова. После презентации своей работы Сару позвали работать в StatDNA.
Позже в конце 2012 лондонский Арсенал выкупил права на американскую компанию почти за 4 миллиона $, а Сара в последствии стала главой департамента аналитики канониров. На данном моменте можно завершить погружение в исторический контекст относительно того, как описываемая математическая теория оказалась востребованной в индустрии футбола, и приступить к непосредственному разбору построенной на ее основе аналитической модели.
Первая модель на основе цепей Маркова (марковская модель) в индустрии футбола
На рисунке ниже приводится условный пример, который разбирается в книге Soccermatics Дэвида Самптера, для демонстрации ключевых особенностей марковской модели, которую изначально предложила Сара.

Все поле разбивается на зоны. Так как изначальная задача модели заключалась в оценке атакующих действий, то основной акцент был уделен финальной трети поля, для которой были выделены 6 зон. Оставшаяся часть поля была помечена отдельной зоной под номером 0.
Вводится понятие - состояние игры. Весь игровой процесс рассматривается как последовательность переходов между различными состояниями. Сара предложила рассматривать такие последовательности переходов как марковские цепи, что позволило использовать основное свойство данного подхода - отсутствие памяти о прошлых состояниях (основное свойство марковских моделей). Другими словами можно сказать, что для марковских процессов вероятности будущих состояний определяются только текущим состоянием процесса и не зависят от прошлых состояний. Безусловно вас может смутить применение данного определения к описанию действий на футбольном поле, т.к. мы знаем, что иногда прошлые состояния в игре могут существенно влиять на то, что будет происходить на поле в следующие моменты времени, но принятое допущение позволяет довольно легко оценивать вероятности будущих состояний игры, в частности вероятность гола (xG), опираясь только на текущее состояние, что в свою очередь упрощает процесс оценки действий футболистов.
Всего в оригинальной модели выделялось 39 состояний.
2 состояния, которые характеризуют окончание процесса владения мячом (гол и потеря мяча)
7 состояний, которым предшествует остановка игры (то что называется Set play, в оригинале у Сары - Set pieces). В данный набор были включены: пенальти, навес с углового, розыгрыш углового, навес со штрафного, розыгрыш штрафного, короткие и длинные вбрасывание из аута.
30 состояний игры, определяемые зоной, в которой находится атакующий игрок с мячом, и расположением обороны соперника (некоторые состояния определяются исключительно зоной, некоторые зоной и оборонительной линией)
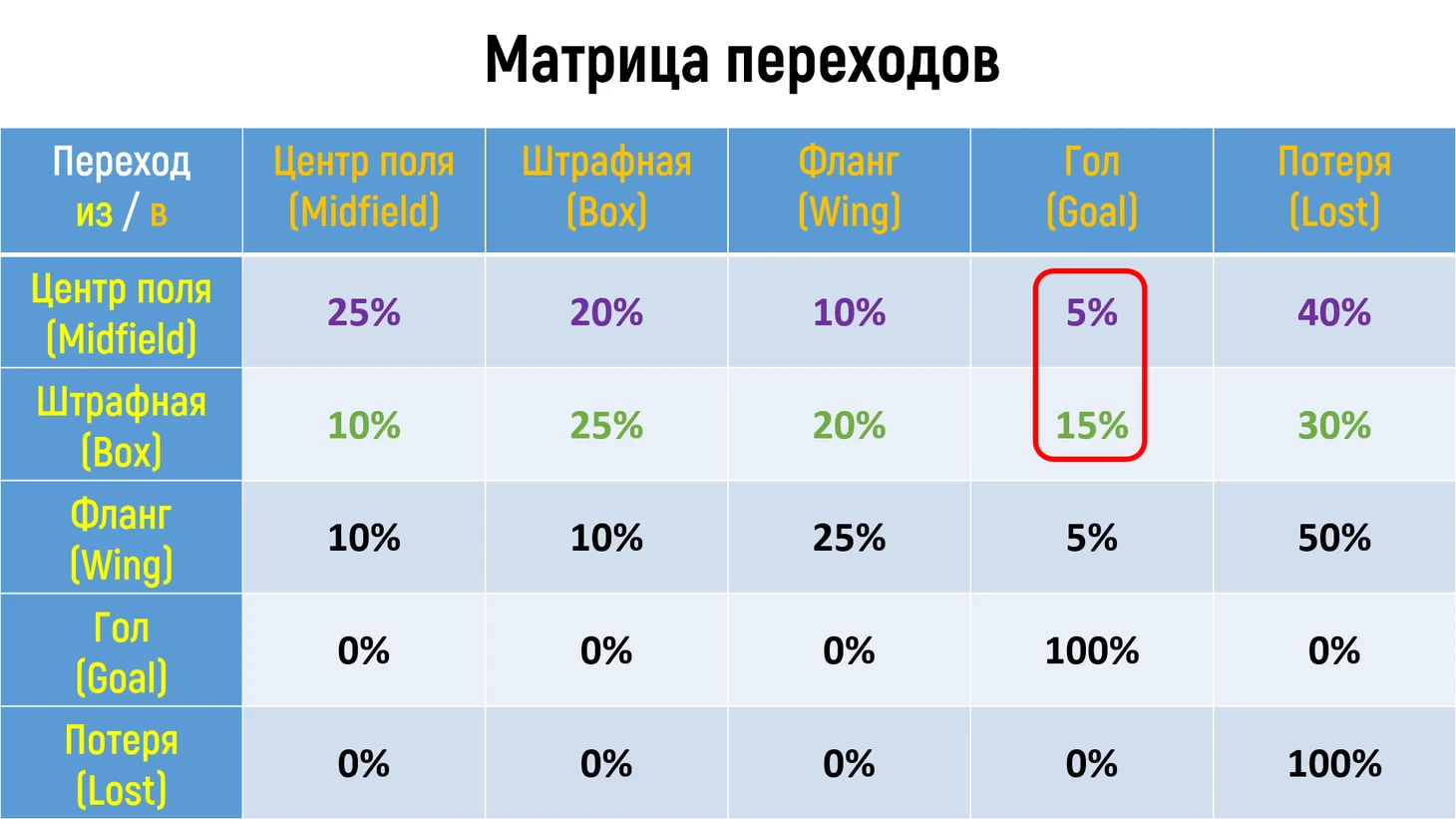
В рассматриваемом примере используются три состояния, которые определяются исключительно зоной, в которой находится атакующий игрок: M - игрок в центре поля, W - игрок на фланге, B - игрок в штрафной. Также в предлагаемом примере указаны два ключевых состояния: G - гол и L - потеря мяча. Оранжевые линии, выходящие из состояния M, указывают все возможные переходы из текущего состояния и соответствующую вероятность (шансы) данного перехода. Т.е. из состояния M доступно 4 перехода в другие состояния и один "переход" обратно в текущее состояние, который соответствует сохранению мяча атакующим игроком. Общая вероятность всех возможных переходов равна 100% (или единице).
В таблице ниже приведены значения вероятностей для различных конечных состояний (колонки с оранжевыми заголовками) в зависимости от исходного состояния (колонки с желтыми заголовками). Данная таблица называется матрицей переходов, значения для которой рассчитываются исходя из статистических данных за рассматриваемый промежуток времени (для рассматриваемого примера статистика может выглядеть следующем образом - все игроки всех команд получали мяч в состоянии M (в центре поля) 100 раз, при этом: 25 раз игрок в данной позиции не отдавал передачи и не бил по воротам (совершал движение с мячом), 20 раз отдавал передачи в штрафную в позицию B, 10 раз на фланг в позицию W, 5 раз бил по воротам и забивал гол и 40 раз команда теряла владение в результате передачи на правый фланг в позицию L. Данный пример - условный, как я говорил ранее, в реальности матрица переходов имела размерность 39 на 39 и учитывала 1521 различный переход.
Способ оценки игроков на основе марковских цепей
Давайте еще раз рассмотрим матрицу переходов. Первая строка соответствует состоянию M и описывает вероятности возможных переходов в другие состояния. Если предположить, что в предыдущий момент времени мяч был отправлен из состояния M в штрафную в состояние B и теперь исходное состояние игры - B, то распределение вероятностей всех возможных конечных состояний, доступных из текущего состояния, можно наблюдать во второй строке, причем мы можем оценить как изменилась вероятность гола (xG) в результате данного действия - xG для нового состояния B минус xG для предыдущего состояния M, что равно 15 - 5 = 10. Т.е. в результате паса из M в B - вероятность гола увеличилась на 0.1 или 10%. По аналогии мы можем оценить изменение вероятности гола для любой пары состояний и как следствие оценить соответствующие действие игрока по увеличению или уменьшению xG в результате данного действия.
Разработанная Сарой модель стала первым инструментом в футбольной аналитике, с помощью которого удалось проводить количественную и качественную оценку атакующих действий футболистов с учетом игрового контекста. Ниже приводится ряд примеров оценивания последовательности действий игроков с помощью модели Маркова. В первом примере рассматриваются 2 передачи и последующий удар. Ранее для такой цепочки действий можно было получить две статистические оценки - голевая передача для игрока 2, и гол для игрока 3. Модель на основе цепей Маркова позволяет:
оценить действие каждого участника атаки в финальной трети поля, а не только двух последних игроков.
провести количественную и качественную оценку для всех пасов в финальной трети поля, т.е. разработанная модель, основываясь на знаке разности xG между двумя состояниями, позволила выделять пасы, которые увеличивают вероятность гола и которые наоборот, снижают опасность.

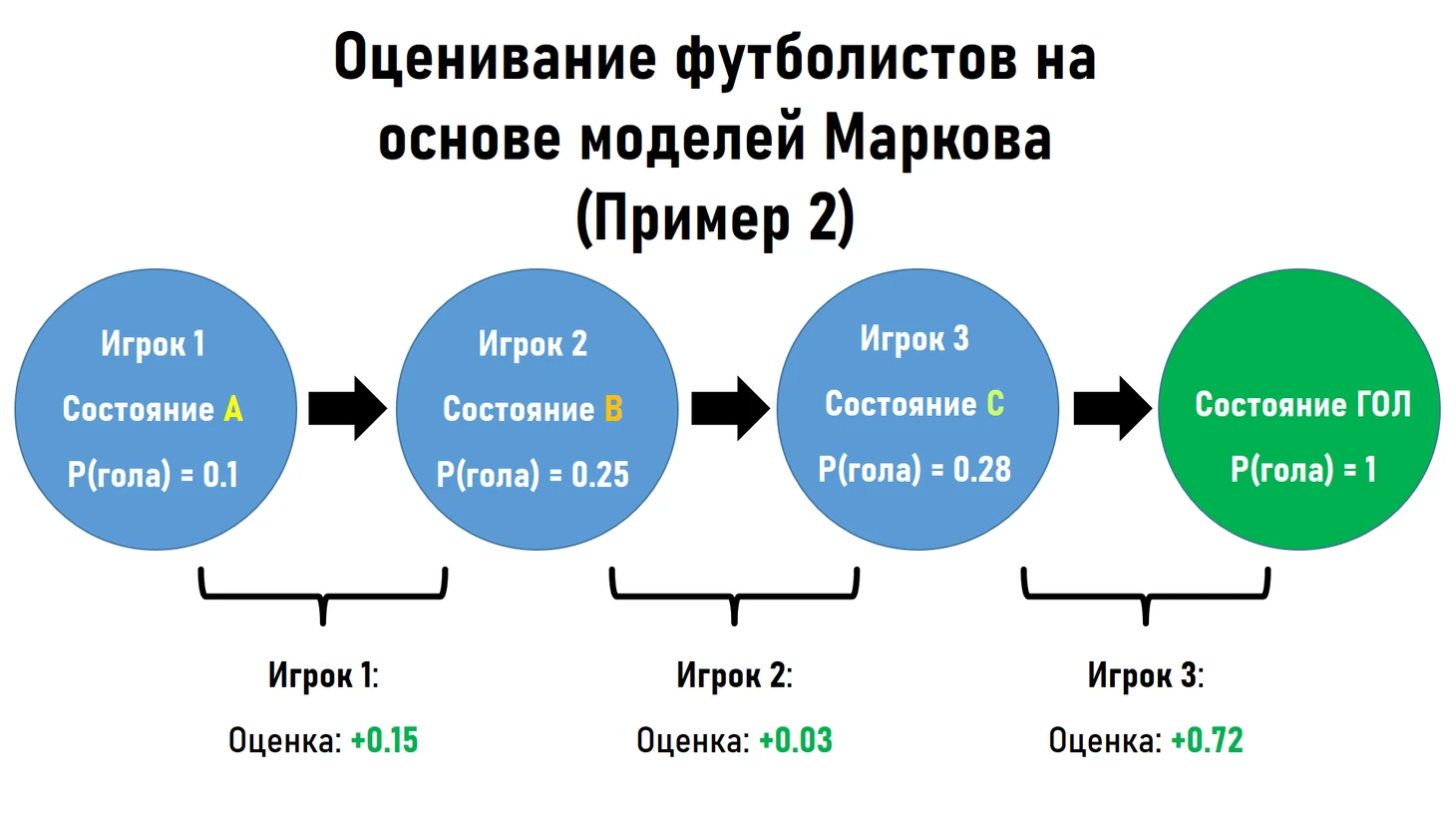
выделять передачи, которые внесли наибольший вклад в увеличение вероятности гола. Во втором примере можно наблюдать, как Игрок 1 получил более высокую оценку в атаке, которая закончилась голом, нежели Игрок 2, который отдал голевую передачу (Ранее действие первого игрока осталось бы вне статистических оценок, а теперь, основываясь на полученной оценке, можно сделать вывод, что действие первого игрока оказалось более весомым с точки зрения увеличения шансов гола, чем непосредственно голевая передача).
количественно оценивать голы, учитывая контекст игры. Т.е. для каждого забитого гола принимается во внимание состояние игры, в котором находился атакующий игрок, забивший гол. Данное состояние, как отмечалось ранее, учитывает и расположение футболиста на поле (зону) и расположение защитников. На примере ниже можно наблюдать, что Игрок 1 забивший гол из более сложной позиции, получил более высокую оценку за забитый гол, нежели Игрок 2, забивший гол из позиции, для которой xG был выше. Ранее оба игрока получили бы одинаковые оценки, которые бы отражали только факт забитого гола.

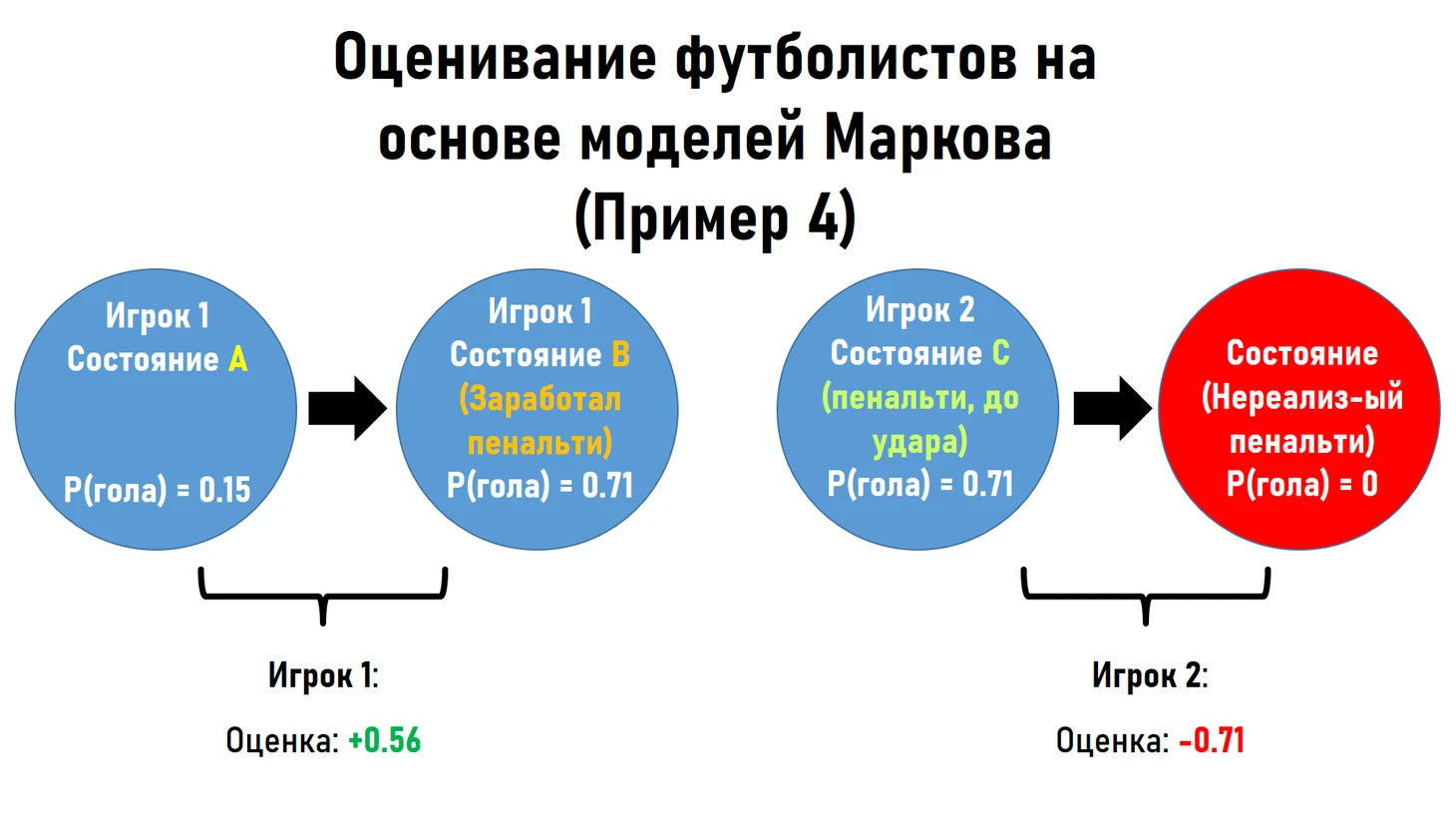
количественно и качественно оценивать атакующие действия игроков, которые ранее не оценивались вовсе или же имели оценки, искажающие фактическую успешность или неуспешность действия. В примере 4 рассматривается ситуация, когда Игрок 1, заработавший пенальти, получает высокую положительную оценку своему действию (ранее данное действие не оценивалось), а игрок 2, не забивший пенальти в результате сэйва вратаря, получает довольно высокую отрицательную оценку для своего действия (ранее данное действие отражалось в статистике как удар в створ, что в итоговой статистике рассматривалось с положительной стороны для всей команды в целом)
Безусловно у фанатов Арсенала есть масса (вполне обоснованных) вопросов к трансферной политике канониров за последние десять лет, основанной во многом на влиянии StatDNA на проводимую селекцию, особенно в период работы Арсена Венгера, но нужно понимать, что несмотря на то что описанные в этой статей статистические подходы для оценки эффективности игроков были революционными для того времени (2011/2012 год) в индустрии футбола и сделали огромный шаг вперед в развитии способов оценивания футбольных статистических данных, они охватывали очень мало игрового контекста и опирались на качество и полноту информации от поставщиков данных о событиях, которые предоставлялись в то время, что в значительной мере ограничивало их эффективность.
За последние десять лет индустрия развивалась очень бурно по всем фронтам. С одной стороны постоянно совершенствовались и обогащались типы собираемых данных и их качество, появлялись новые крупные игроки на этом рынке (если интересно узнать больше о типах футбольных данных и особенностях инструментов на их основе, то можете найти инфу здесь). С другой стороны развивались сами методы - появлялись более сложные модели на основе уже известных подходов (в частности на основе цепей Маркова, которые будут рассмотрены далее) и совершенно новые подходы на основе машинного обучения, например, метрика VAEP, которая описывалась в одной из моих статей.
Современные модели на основе цепей Маркова
Февраль 2019 года ознаменовался сразу двумя громкими анонсами в мире футбольной аналитики, которые интересны нам в контексте модели, описанной ранее. 15 февраля Карун Сингх (Karun Singh) презентовал в своем твиттере новую метрику xT (Expected Threat - Ожидаемая угроза), которая подробно была описана в одной из статей на sports.ru, а 21 февраля StatsBomb анонсировали новую модель для оценки атакующих действий игроков, назвав ее Ball Progression Model - модель продвижения мяча и рассчитываемую на ее основе метрику - Attacking contribution (атакующий вклад). Обе предложенные модели основаны на все тех же цепях Маркова, которые мы рассмотрели ранее.
Описание модели Ball Progression Model (BPM) и метрики Attacking contribution
StatsBomb в своей публикации в явном виде указывают, что их модель является развитием модели разработанной Сарой в 2011 году. На рисунке ниже представлен способ разделения футбольного поля на зоны. Можно наблюдать, что теперь модель оценивает действие совершенное в любой точке поля, а не только в финальной трети, как было в оригинальной модели Сары.

Ниже будут перечислены основные особенности модели, разработанной StatsBomb.
В BPM также как и в модели Сары рассматриваются два специальных состояния, которыми может закончится цепочка владения мячом, - гол и потеря мяча, все остальные состояния считаются переходными (всего 84 переходных состояний игры)
Среди переходных состояний выделяются 8 специальных состояний, которым предшествует остановка игры. Штрафные удары в каждой трети поля (атакующая треть, середина, оборонительная треть), вбрасывания аута в каждой трети поля, угловые удары и заработанные пенальти.
Остальные переходные состояния определяются исключительно зоной поля и наличием или отсутствием давления со стороны соперника в данной зоне. Т.е. в модели BPM выделяют 38 состояний (по количеству зон) для случаев наличия давления и столько же состояний для случаев отсутствия давления.
Цепочка владения может включать любое количество переходных состояний
Вероятность следующего переходного состояния определяется только текущим состоянием и не зависит от прошлых (здесь мы понимаем, что для описания процесса используются цепи Маркова) Т.е. если мы находимся в зоне 21, то вероятность паса в зону 28 будет одинаковой для любых предыдущих состояний (в независимости от того, пришел пас из зоны 11, 14 или 22, например)
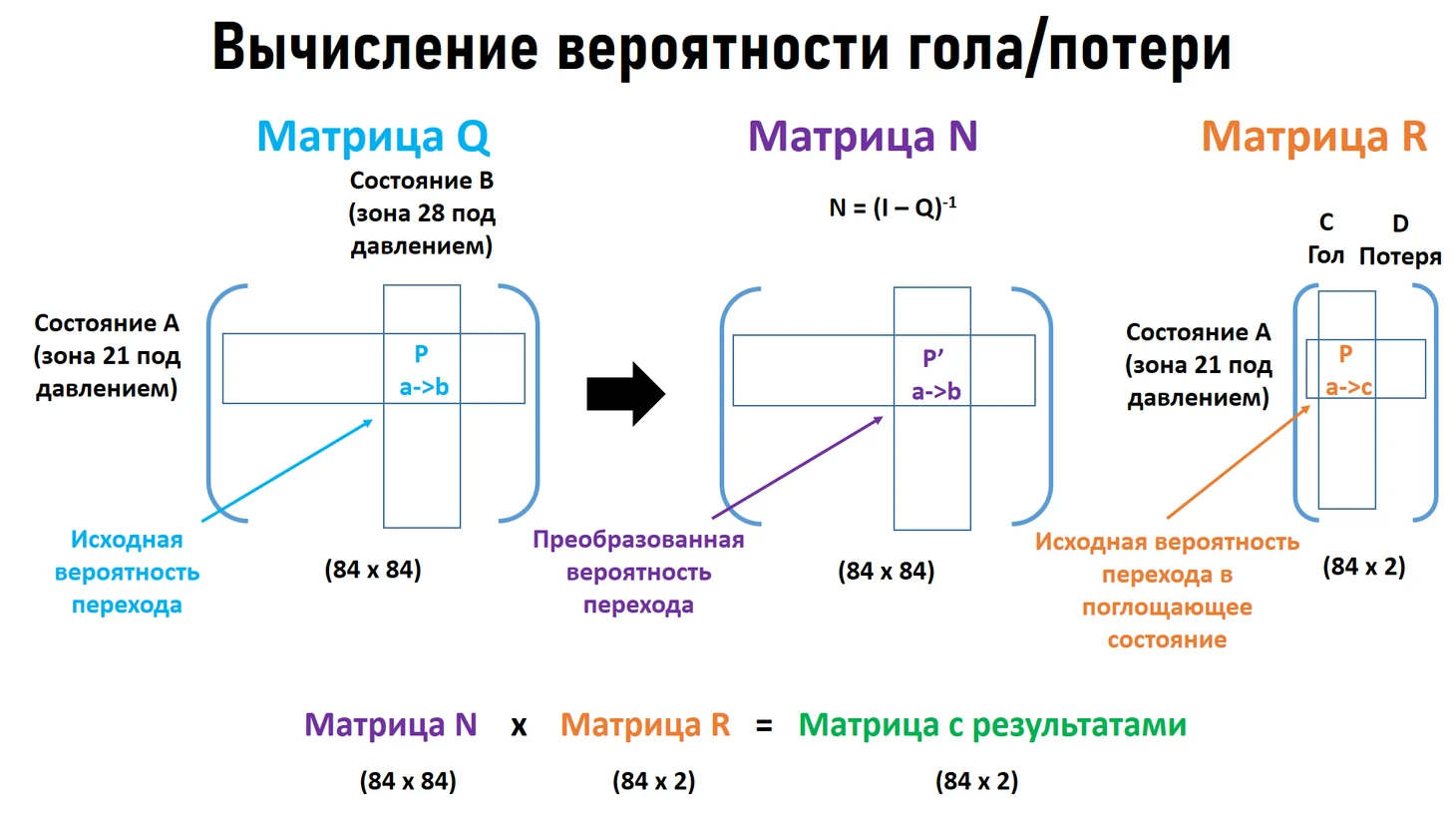
Для всех переходных состояний строится матрица переходных вероятностей Q размером 84 x 84, в каждой ячейке которой указывается вероятность перехода из переходного состояния A в переходное состояние B. Для двух специальных состояний, которые еще называются absorbing states (поглощающие состояния - т.е. состояния, из которых нельзя попасть ни в какое другое, и вероятность которых равна 1), строится отдельная матрица поглощающих вероятностей R размером 84 x 2, в каждой ячейке которой указывается изначальная вероятность перехода из переходного состояния A в поглощающее состояние C. Далее на основе матрицы Q рассчитывается фундаментальная матрица N путем несложных преобразований линейной алгебры, которые здесь опустим.
В результате, на основе построенных матриц для каждого переходного состояния можно рассчитать ожидаемое количество атакующих действий (пасы, ведение мяча, удары) через которое будет достигнуто одно из поглощающих состояний (гол или потеря мяча) и непосредственно вероятности поглощающих состояний в следующий момент времени (т.е. вероятности того, что следующие состояния станут поглощающими). На рисунке ниже схематично представлены используемые матрицы и проводимые вычисления. Финальные вероятности, используемые далее в метрике attacking contribution содержаться в матрице с результатами, которая имеет ту же размерность что и матрица R.
Результаты применения BPM
Описанная выше модель тестировалась на данных о событиях Топ-5 европейских чемпионатов, Чемпионшипа и Первой лиги Англии сезонов 2017-2018 и 2018-2019. Для каждого из 84 переходных состояний были рассчитаны вероятности гола и потери мяча в следующем состоянии и количество действий до соответствующих поглощающих состояний (т.е. количество действий до момента когда вероятность гола или вероятность потери равна единице). В результате данных вычислений удалось выделить следующие состояния (зоны) с наибольшей вероятностью гола:
Зона 36 с давлением - P(Goal) = 19.2% (xG = 0.192)
Зона 31 с давлением - P(Goal) = 9% (xG = 0.09)
Зона 36 без давлением - P(Goal) = 8.3% (xG = 0.083). Данный результат кажется контринтуитивным, т.к. выше мы видели, что вероятность гола из аналогичной зоны при наличии давления со стороны соперника несколько выше. Здесь может иметь место как ошибка в номере зоны в оригинальной публикации, так и демонстрация парадоксальности полученных результатов на основе используемой статистики. Можно предположить, что количество ситуаций, когда атакующий игрок оказывался в зоне 36 (вратарская площадь) без давления, очень мало в собранной статистике (относительно состояний с давлением) и в таких ситуациях игроки чаще упускают шанс забить гол (например, замыкание сильного прострела).
В качестве состояний с наибольшей вероятностью потери были отмечены зоны 1, 2 и 3 с давлением, для каждой из которых вероятность потери равна 99.5%.
На рисунке ниже представлена цепочка владения, которая закончилась голом. Для каждого переходного состояния в данной цепочке приведено значение метрики contribution, которая оценивает атакующий вклад совершенного действия с точки зрения увеличения вероятности гола и рассчитывается как разность xG изначального и конечного состояний. В рассматриваемом примере нулевое значение соответствует сохранению значения xG в результате действия, отрицательные значения - снижению шансов, а положительные - повышению (данный пример - демонстрационный, в нем опущена информация относительно наличия или отсутствия давления для каждого переходного состояния в рассматриваемой цепочке).
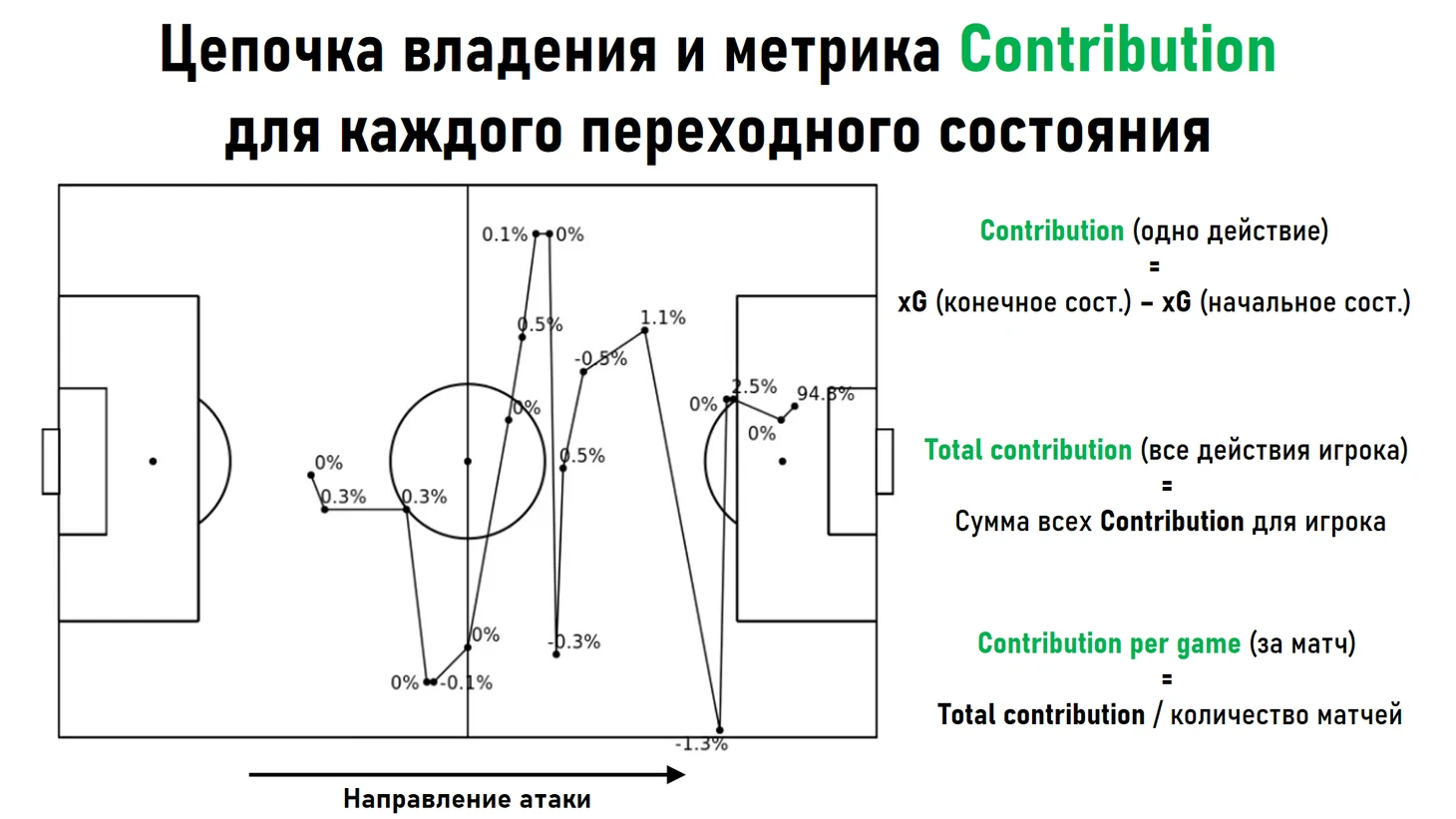
Для каждого конкретного игрока можно сложить значения contribution по всем действиям и разделить полученный результат на количество сыгранных матчей, в результате чего получить производную метрику - Contribution per game (атакующий вклад игрока за матч в среднем).
В таблицах ниже представлены рейтинги пяти лучших игроков для различных позиций (нападающий, полузащитник, защитник и голкипер) по метрике Contribution per game (CPG), полученные на основе марковской модели, разработанной StatsBomb на основе статистики за указанные ранее сезоны. (т.е. актуально на февраль 2019)
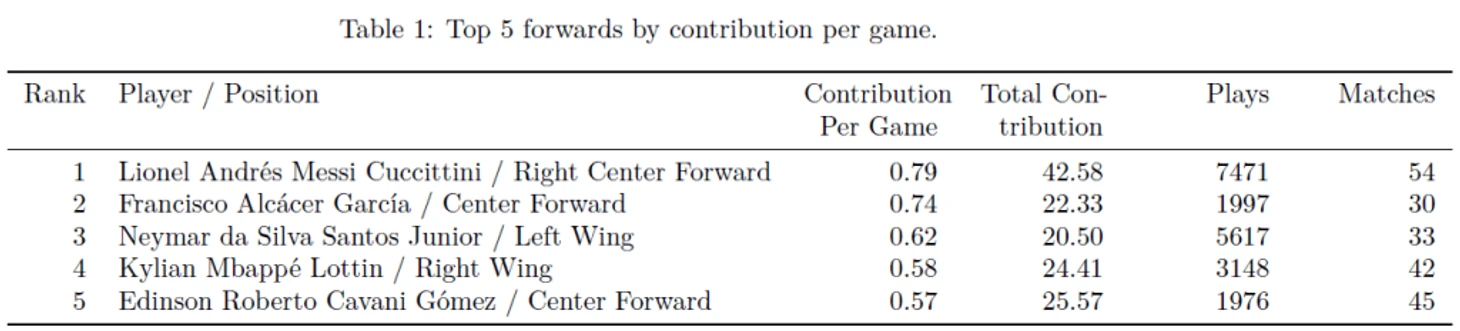
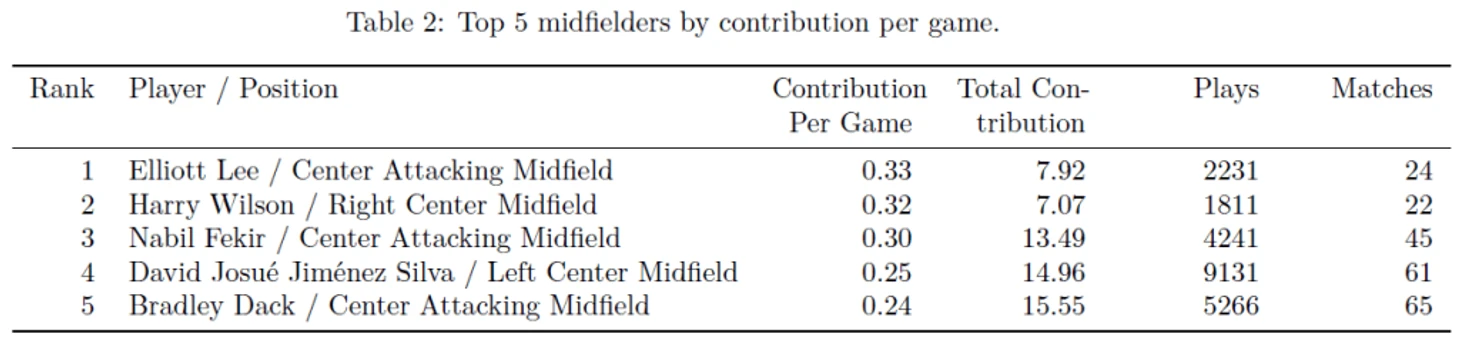
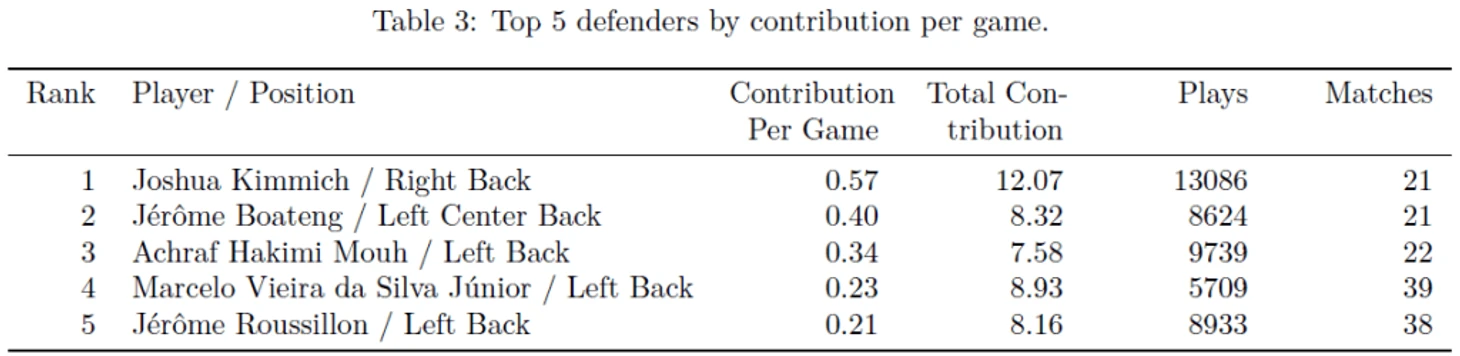
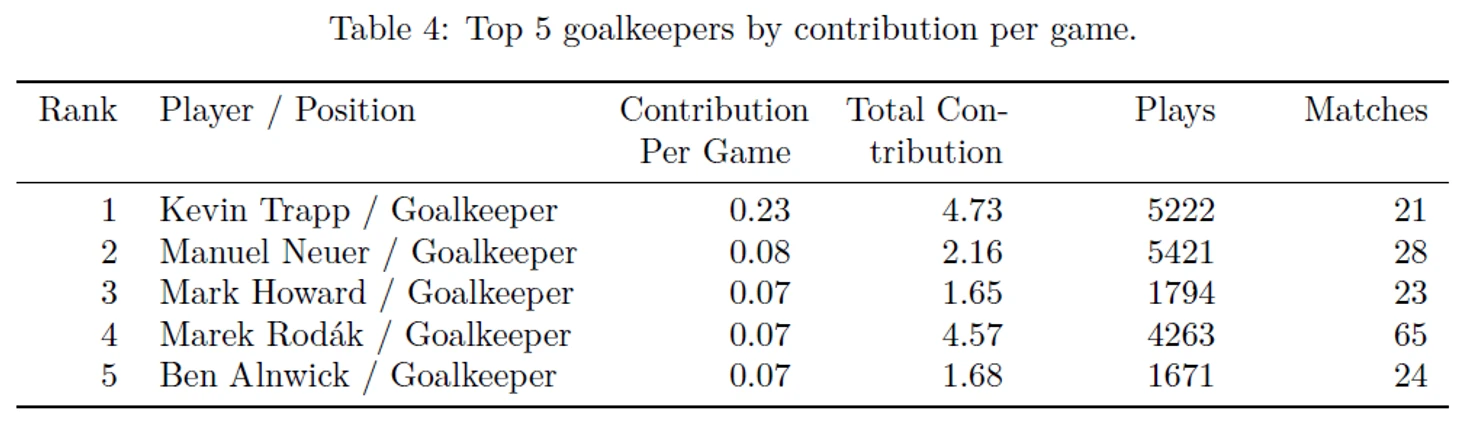
В данном рейтинге есть ряд футболистов, которых вы можете не знать, это:
Эллиот Ли, выступавший в сезоне 2018-2019 году за Лутон в первой лиге Англии, который стал чемпионом в том сезоне и заработал путевку в Чемпионшип. Эллиот набрал 15 очков по системе гол + пас в том сезоне и стал лидером по метрике CPG среди полузащитников (играл как чистого нападающего, так и атакующего полузащитника).
Харри Уилсон, воспитанник Ливерпуля, набрал 10 очков по системе гол + пас в сезоне 2017-2018 в аренде за Халл в Чемпионшипе и 20 очков в следующем сезоне в очередной аренде за Дерби Каунти (также в Чемпионшипе). В рейтинге лучших полузащитников занял второе место.
Брэдли Дэк, выигравший в сезоне 2017-2018 в составе Блэкберна первую лигу Англии, при этом набрав 26 очков (гол + пас). В следующем сезоне Брэдли продолжил свое выступление за Блекберн, показав также довольно хороший результат - 22 очка. Брэдли замыкает рейтинг пяти лучших полузащитников.
Жером Руссийон, попавший в компанию лучших защитников (по метрике CPG) к Киммиху, Боатенгу, Хакими и Марсело, в сезоне 2017-2018 набрал 7 очков с Монпелье в первой лиге Франции и уже в следующем сезоне повторил свой результат в Германии с Вольфсбургом.
Марк Ховард - голкипер, выступавший в сезоне 2017-2018 за Болтон в первой лиге Англии и за Блэкпул в Чемпионшипе в сезоне 2018-2019.
Марек Родак - голкипер, выступавший за Ротерхэм в первой лиге в сезоне 2017-2018 и в Чемпионшипе в следующем сезоне.
Бен Эник - голкипер, выступавший за Питерборо и Болтон в сезоне 2017-2018 в первой лиге Англии и продолживший свою карьеру в Болтоне в следующем сезоне (также в рамках первой лиги Англии)
Аналитики из StatsBomb преднамеренно не стали нормализовывать метрику CPG на "силу чемпионата" и оставили рассчитанные значения в изначальном (сыром) виде. В результате мы получили пятерку лучших полузащитников полностью состоящую из игроков Чемпионшипа и первой лиги Англии, в которых набрать более высокие балы более легко, чем в топ 5 европейских дивизионов (т.е. contibution для одного и того же действия в разных лигах имеет разную значимость, т.к. отличается класс игроков, уровень давления и скорости игры). Данный подход может быть полезен для поиска молодых талантов в низших лигах. В случае введения поправочных коэффициентов для метрики, рейтинги футболистов из низших дивизионов с большой вероятностью будут перекрыты рейтингами игроков из более сильных лиг.
Разработанная StatsBomb модель на основе цепей Маркова довольно хорошо позволяет определять наилучших футболистов по количеству и качеству атакующих действий. Результаты полученные с помощью BPM легко интерпретируемы для людей далеких от статистики и профессиональной аналитики (в отличие от моделей на основе машинного обучения, например, все та же метрика VAEP). Тем не менее у данной модели есть ряд ограничений:
Использование основного свойства марковских моделей (отсутствие памяти о прошлых состояниях) предполагает, что каждое последующее состояние в цепочке владения мячом не зависит от предыдущих, хотя в реальности такая зависимость безусловно есть. StatsBomb занимается развитием модели BPM и указывает на то, что в будущих реализациях будут использованы цепи Маркова более высокого порядка, которые позволяют обойти указанное ограничение (не будем вдаваться в подробности, просто нужно понимать, что есть самые простые модели на основе цепей Маркова, в которых есть указанное ограничение, и есть более сложные цепи Маркова, в которых данное ограничение отсутствует, т.е. такие модели могут учитывать прошлые состояния)
Разработанная модель не учитывает тип действия, которое выполняется при переходе из одного состояния в другое. Т.е. модель рассчитывает вероятность перехода из одного состояния в другое, но не учитывает тот факт, что переход может быть совершен в результате паса или дриблинга, например. По идее, вероятности гола (xG) в новом состоянии при переходе в результате действий различных типов должны отличаться. Данную особенность можно учесть введением фиксации времени перехода из одного состояния в другое (например, при пасе переход будет более быстрым, чем при простом движении с мячом/дриблинге). Такие модели на основе цепей Маркова с учетом времени перехода уже реализованы в теннисе, баскетболе и хоккее.
Разработанная модель на основе цепей Маркова предлагает дискретную структуру переходных и поглощающих состояний. Т.е. футбольный матч рассматривается в виде набора отдельных переходов между различными состояниями в одно из конечных состояний. Данный подход еще называют дискретным случайным процессом. Указанная особенность приводит к потере полезной информации о процессе, т.к. футбол является игрой с довольно "плавно" меняющимися состояниями, в отличие, например, от американского футбола, бейсбола или крикета, которые можно отнести к более дискретным играм (т.е. прерывистыми, разбитыми на множество отдельных эпизодов). Данное ограничение можно обойти используя специальные методы, которые позволяют рассматривать марковские цепи в качестве непрерывного случайного процесса, но такие методы значительно усложняют модель и ее простую интерпретацию для широкой публики.
Рассмотренная выше BPM является фундаментом для более полноценной марковской модели, в которой будут разрешены указанные выше ограничения. Не знаю на каком этапе в данный момент находится реализация анонсированной модели (более полноценной BPM), но два года назад StatsBomb активно развивал данный инструмент.
xT (Expected Threat - ожидаемая угроза)
Как я указывал ранее, метрика xT уже была подробно описана на sports.ru, поэтому я рассмотрю только ключевые моменты данного инструмента, отражающие ее связь с работой Сары и цепями Маркова.
Введение в модель, позволяющую оценивать ожидаемую угрозу от совершенного атакующего действия, начинается с общего анализа моментов игры, в которые команда владеет мячом и находится в состоянии атаки (в английском языке данная фаза игры называется - buildup play; для оценки действий в данной фазе игры существует специальная метрика xGBuildup, о которой можно почитать здесь). Проделанный анализ был основан на данных о событиях АПЛ сезона 2017-2018. В проведенном анализе все поле разбивалось на 192 зоны и для каждой зоны на основе собранной статистики была рассчитана вероятность перехода в любую другую зону (т.е. была составлена уже известная нам матрица переходов), в том числе вероятность удара по воротам и непосредственно вероятность гола.
На слайде ниже представлен пример работы построенной модели для оценки того, как может развиваться игровая ситуация в атакующей фазе игры, если игрок находится с мячом в зоне А. Можно наблюдать, что с вероятностью 0.3 из зоны А последует удар, и с вероятностью 0.7 будет совершен перевод мяча в одну из выделенных зеленых зон (в результаты паса другому футболисту или продвижению игрока с мячом), причем, чем более ярко выделена зона, тем выше соответственная вероятность перехода. При этом, вероятность гола в данной зоне (xG) составляет 0.02.
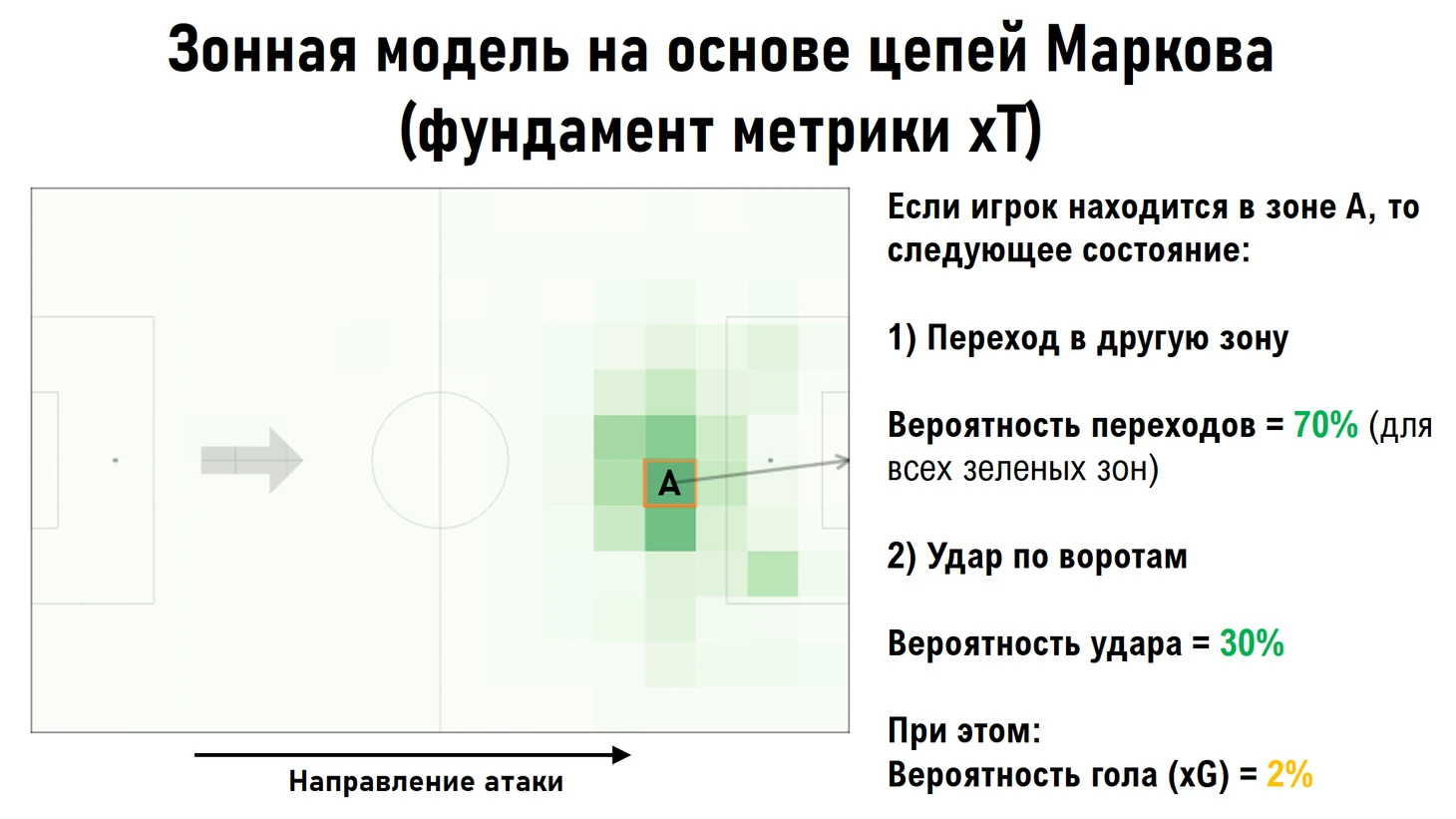
Как вы могли заметить, в основе построенной модели используется все тот же подход, который ранее был использован в модели Сары - описание игрового процесса в виде последовательности переходов между различными состояниями, вероятность которых рассчитывается для собранной статистики, причем для каждой новой зоны вероятности распределяются независимо от того, как мяч попал в данную зону, т.е. используется все тоже основное свойство простых марковский цепей - отсутствие памяти о прошлых состояниях.
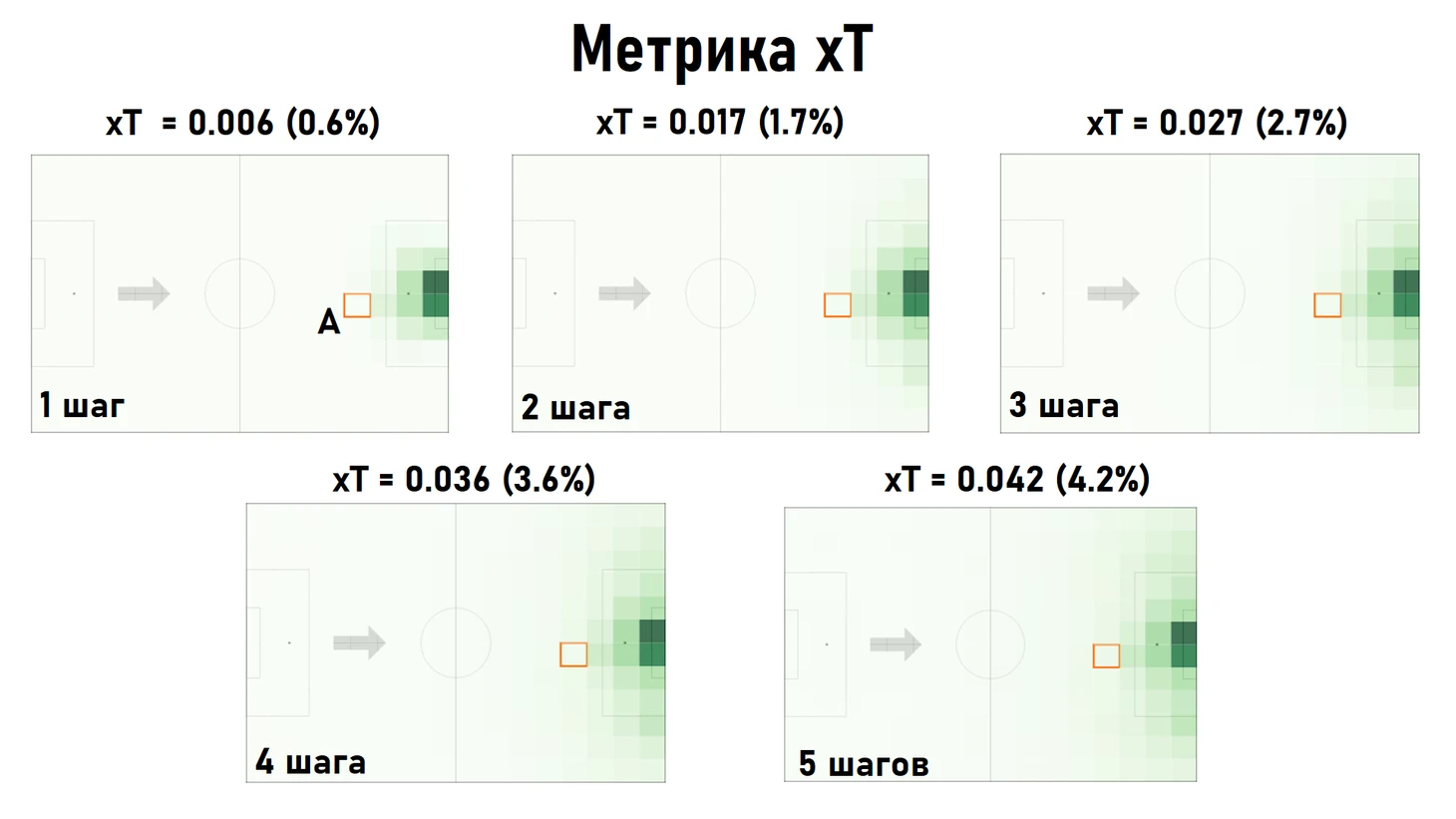
На основе рассмотренной модели вычисляется показатель xT для каждой указанной зоны, позволяющий оценивать вероятности того, что через несколько следующих действий будет забит гол (обычно через 4-5 действий), если игрок находится в определенной зоне. Данное значение рассчитывается для каждой зоны. На слайде ниже изображены футбольное поле и соответствующие значения метрики xT для зоны А для моделей, учитывающих различное количество действий до гола. Чем более яркий раскрас имеет зона, тем более высокое значение xT ей соответствует.
Можно наблюдать, что:
при увеличении числа последующих действий в модели, увеличивается соответствующая вероятность гола, что выглядит довольно логично (т.е. если мы находимся в зоне А, то вероятность того, что в следующее состояние будет забит гол, равна 0.6% (первая картинка), и если мы находимся в зоне А, то вероятность того, что через 5 следующих действий будет забит гол - 4.2% (последняя картинка))
при увеличении числа последующих действий в модели, увеличивается количество зон вокруг ворот, которые окрашиваются в более яркий зеленый цвет, т.е. увеличивается количество зон, для которых значение метрики xT значительно превышает 0, что также выглядит довольно логично, т.е. чем больше действий мы закладываем в модель, тем больше вариативность зон, из которых может стартовать опасная цепочка владения, имеющая потенциал закончиться взятием ворот.
Метрика xT вычисляется по не совсем простой формуле, детальный разбор которой значительно перегрузит и так не самую легкую для восприятия широкой аудиторией информацию, поэтому опустим объяснения. Основная задача следующего слайда заключается в том, чтобы продемонстрировать, как связаны показатели, которые рассчитываются зонной моделью на основе марковских цепей, и результирующая метрика. Ниже я структурно обозначил основные составляющие, которые используются при вычисления xT для каждой зоны поля.
Можно наблюдать, что xT опирается на вероятности удара, вероятности переходов в другие состояния и непосредственно xG (показатели, выделенные цветом).

Ниже разбирается пример, в котором демонстрируется способ оценки атакующих действий игроков, опираясь на рассчитанные значения xT для каждой зоны футбольного поля. Для каждого совершенного действия вычисляется разность значений xT (xT Created / созданная опасность) для конечной и начальной зоны, данная разность является финальной оценкой, которую получает игрок за совершенное действие. Также оценка xT для каждого действия позволяет оценивать процентный вклад игроков в созданный голевой момент. В рассмотренном примере из двух передач и последующего удара, который привел к голу, использование метрики xT позволяет выделить действие Игрока 1, вклад которого составил 72% в общую опасность созданную совместно Игроком 1 и Игроком 2, совершившим голевую передачу.

Общий вывод:
Марковские модели являются одним из самых эффективных способов оценки атакующих действий футболистов на поле. Первая модель на основе цепей Маркова, предложенная широкой аудитории в 2011 году, заложила фундамент для других, более сложных моделей, которые продолжают развиваться в настоящее время (xT, Contribution). Рассмотренные инструменты имеют ряд ограничений, которые снижают качество получаемых оценок из-за потери информации о игровом процессе, что оставляет потенциал для дальнейшего улучшения (дальнейшее усложнение рассмотренных моделей). Основным конкурентом моделей на основе цепей Маркова остается метрика VAEP, полученная на основе применения моделей машинного обучения (сравнение VAEP с метрикой xT было проведено здесь)
P.s. Если интересно следить за обновлениями, но вы не зарегистрированы на sports.ru, то подписывайтесь на инстаграм блога или группу в вк.












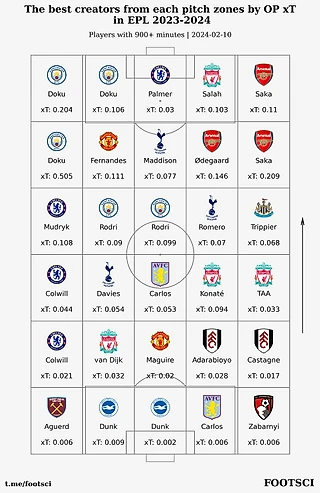
А с помощью этих метрик теперь можно выделить скрытых героев, те которые на протяжении всего сезона стабильно улучшают вероятность гола своими действиями, но при этом даже не попадают в обзоры матчей, тк нарезка обычно включает сам гол и пас передним ним, а иногда и голевой пас не включает.
Ну и больше данных для комментаторов, нам интереснее слушать и обращать внимание еще и на теневых героев команд. Но в целом, это конечно тул в первую очередь для тех кто занимается скаутингом.
Вот еще один обзор по данной метрике. В нем рассматриваются все матрицы переходов, которые удалось найти в свободном доступе, и которые активно используются в любительской аналитике. Плюс строится новая матрица переходов, на основе которой формируется ряд рейтингов.
https://www.sports.ru/tribuna/blogs/footsci/3201710.html
А сами значения метрик можно рассчитать по координатам event-данных, спарсеных с whoscored.com.
Работаю продуктовым аналитиком. И в работе использую библиотеку Retentioneering (https://retentioneering.com/). Она строит графы, матрицы переходов, делает кластеризацию и проч. Как-то поигрался с ней применительно к евент-данным. Добавил сущность "владение". И собрал графы вледений, кластеризировал. Толку было немного, но интересно это все покрутить.
К сожалению, не всем даны такие аналитические способности как вам, увы.
Если вы меньшим количеством букв сможете описать что-нибудь, что принесет пользу для понимания футбола, то пришлите ссылку, я с удовольствием прочитаю.
А если не перепутали , тогда почему такие умники как вы не вывели российский футбол на качественный уровень ?! Вы же все знаете о футболе. Аналитики ....
-----------------
а что мешает сделать 2 разных топа или даже больше с разными поправками? Один для топ-лиг, другой для нетоповых, отдельно для низших лиг? А то всё смешалось - кони и люди, козы и капуста)
Для человека, который занимается аналитикой поверхностно, самое главное - это описание метрик по сути, а также ссылки на сайты, где эти метрики можно добыть БЕСПЛАТНО. Второй момент у вас не раскрыт. Если эти данные нельзя найти в свободном доступе, на этом нужно сделать акцент.