С помощью Glicko-2, LightGBM и xG прогнозируем результаты матчей большой пятерки
В первой статье этого блога мы смоделировали результаты несостоявшихся матчей французской Лиги 1. Тогда мы использовали модель Glicko-2, которой скармливали результаты сыгранных матчей, на основе которых предсказывали результаты несостоявшихся игр. В конце статьи мы пришли к выводу, что было бы неплохо использовать не только результаты матчей, а также данные по xG. В этой статье мы построим фактически три модели: Glicko-2 на основе результатов матчей, Glicko-2 на основе xG, а также обучим алгоритм LightGBM на данных по голам и xG. После усредним прогнозы, закинем результаты в метод Монте-Карло и посмотрим, что получилось.
Данные
Будем использовать данные за последние четыре сезона, включая текущий. Источником послужит сайт fbref.com. Данные представляют собой результаты матчей, а также статистику по xG.
Glicko-2 на основе результатов матчей
Модель Гликмана является рейтинговой системой. Команды начинают сезон с одинаковым рейтингом. Рейтинг – это положительное число: если команда побеждает, ее рейтинг растет, если проигрывает – рейтинг падает. Изменение рейтинга зависит от уровня соперников:
если побеждает фаворит, то оппоненты подтвердили результатом отношение своих рейтингов до игры, поэтому нет смысла существенно обновлять их рейтинги;
если побеждает андердог, то рейтинг надо существенно обновить, потому что рейтинги до игры не отображали истинного соотношения сил;
если матч заканчивается вничью, то андердог получает очки рейтинга, а фаворит теряет очки рейтинга.
Также мы вводили в модель параметр преимущества домашнего поля. Таким образом модель учитывает сложность календаря команд.
Подробнее можно почитать в той же статье про Лигу 1, а также в статьях, где мы составляли рейтинг европейских лиг: тут и тут.
Glicko-2 на основе xG
Однако у вышеописанного подхода есть существенный недостаток. Хорошие результаты не всегда отражают хорошее качество игры. Здесь нам поможет xG. Поступим следующим образом. При пересчете рейтингов будем использовать не реальные исходы, а исходы на основе xG. Если одна из команд «перепинала» другую на более, чем 0.5 xG, то засчитываем ей победу. Если разница по xG меньше 0.5, то засчитываем ничью. Мы по-прежнему пытаемся предсказать реальный исход матча, только делаем это на основе данных по xG. Так мы учитываем качество игры в предыдущих матчах.
LightGBM и распределение Скеллама
Однако у нас осталась еще парочка проблем. Две предыдущих модели строятся на «победах/ничьих/поражениях». Они игнорируют информацию о разгромных победах. Победа 5:0 моделью Гликмана оценивается также как и победа 1:0. Также Glicko-2 плохо прогноризует ничьи. В модели вероятность ничьи зависит от разницы рейтингов команд и параметра draw_inclination, который одинаков для всех команд в одном чемпионате. На практике вероятность ничьи зависит не только от уровня соперников, а также от их результативности. Если команды низкорезультативные, вероятность ничьи выше.
Строить модель будем, используя знание, что голы в футболе имеют распределение Пуассона. Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона.
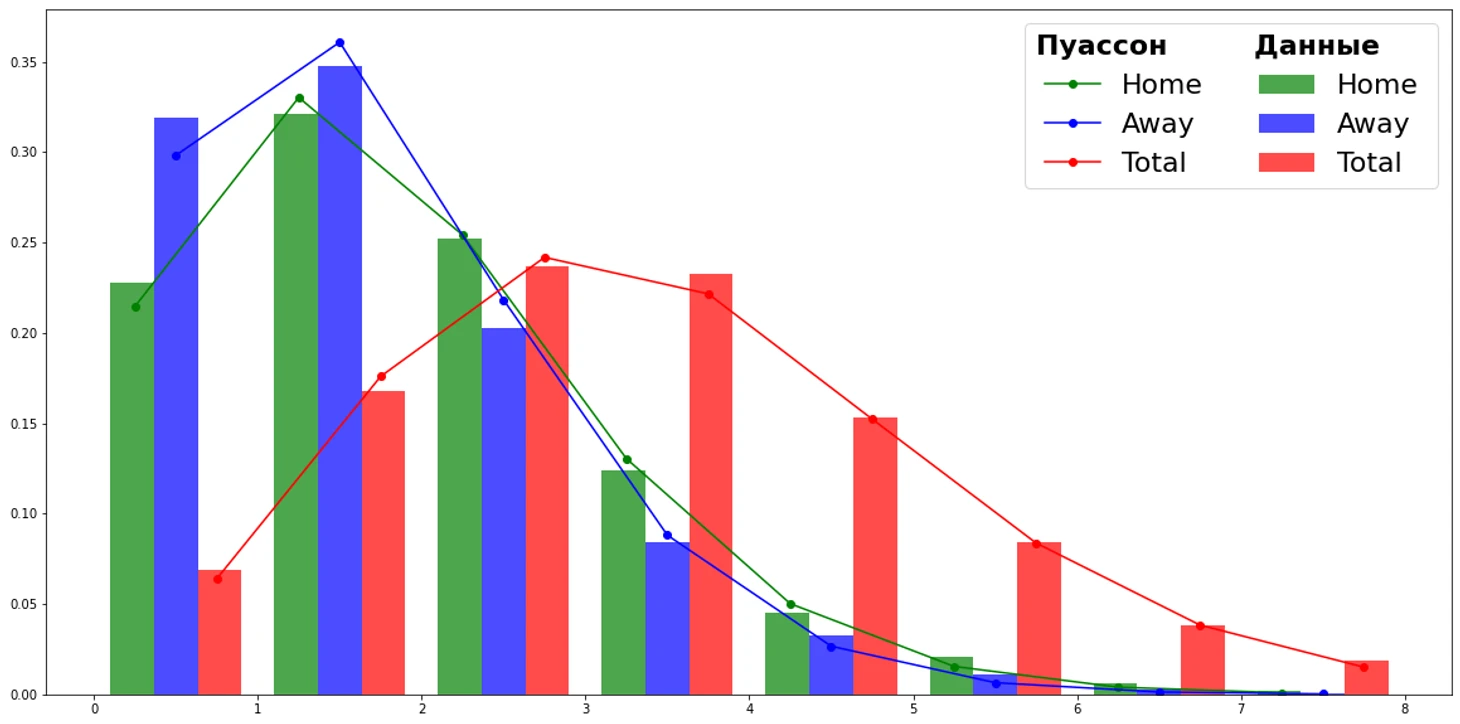
Но в футболе побеждает тот, кто забивает больше и пропускает меньше. Поэтому нам интересна разница голов, а она имеет распределение Скеллама.
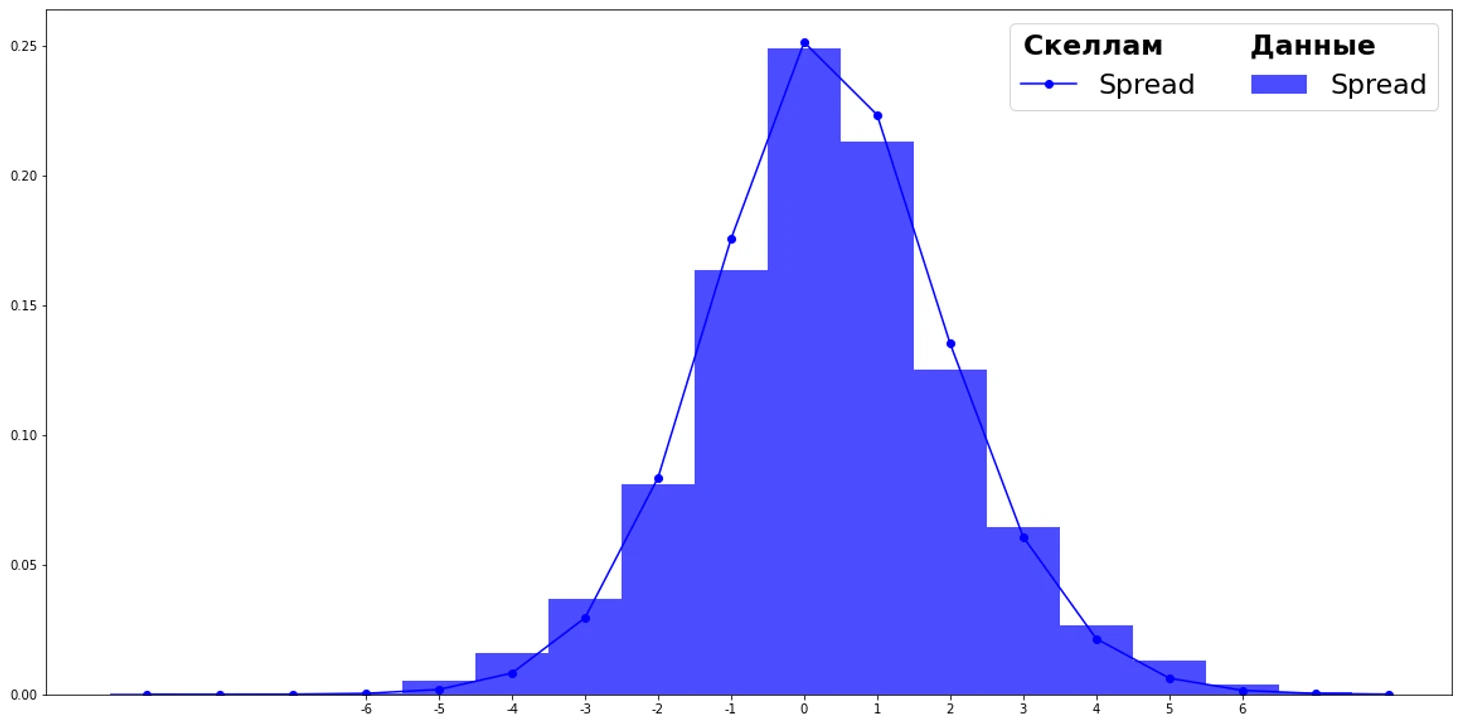
Поступим следующим образом. Научим модель LightGBM прогнозировать количество голов, которое забьет команда. В качестве objective укажем poisson, так как целевая переменная (голы) распределена по Пуассону. Для каждого матча получим два прогноза количества голов для домашней и гостевой команды. Фактически данные прогнозы являются математическими ожиданиями голов, которые мы можем использовать в качестве параметров для функции вероятности Скеллама.
p(k, m1, m2) – функция вероятности Скеллама, где
k – значение разницы голов.
m1 – матожидание голов (прогноз LightGBM) домашней команды.
m2 – матожидание голов гостевой команды.
Например, p(1, 1.9, 0.8) означает вероятность домашней команды выиграть в один гол, при матожидании 1.9 гола и матожидании соперника 0.8. Если просуммировать вероятности вида p(1, m1, m2) + p(2, m1, m2) + p(3, m1, m2) + ..., получим вероятность победы хозяев поля, p(0, m1, m2) – вероятность ничьи, p(-1, m1, m2) + p(-2, m1, m2) + p(-3, m1, m2) + ... – вероятность победы гостей. Таким образом мы получим прогноз на исход матча.
Для обучения LightGBM будем использовать следующие признаки:
Айдишник команды для которой делаем прогноз количества голов.
Айдишник соперника.
Играет ли команда дома.
Среднее количество голов, которое команда/соперник забивает/пропускает.
Средний xG, который команда/соперник создает/позволяет создавать.
Производные признаки от вышеперечисленных.
Обучение моделей
Давайте подберем параметры, при которых модели показывают наилучшую точность. Все три модели предсказывают исход матча, поэтому логично выбрать метрику log loss в качестве меры точности моделей, чем меньше это значение, тем модель лучше. Подбирать параметры будем на данных последних трех сезонов большой пятерки.
Для Glicko-2 подбираем начальное значение параметра rating deviation, параметр преимущества домашнего поля и параметр склонности сыграть вничью. Для LightGBM подбираем гиперпараметры.
Получили следующие результаты.
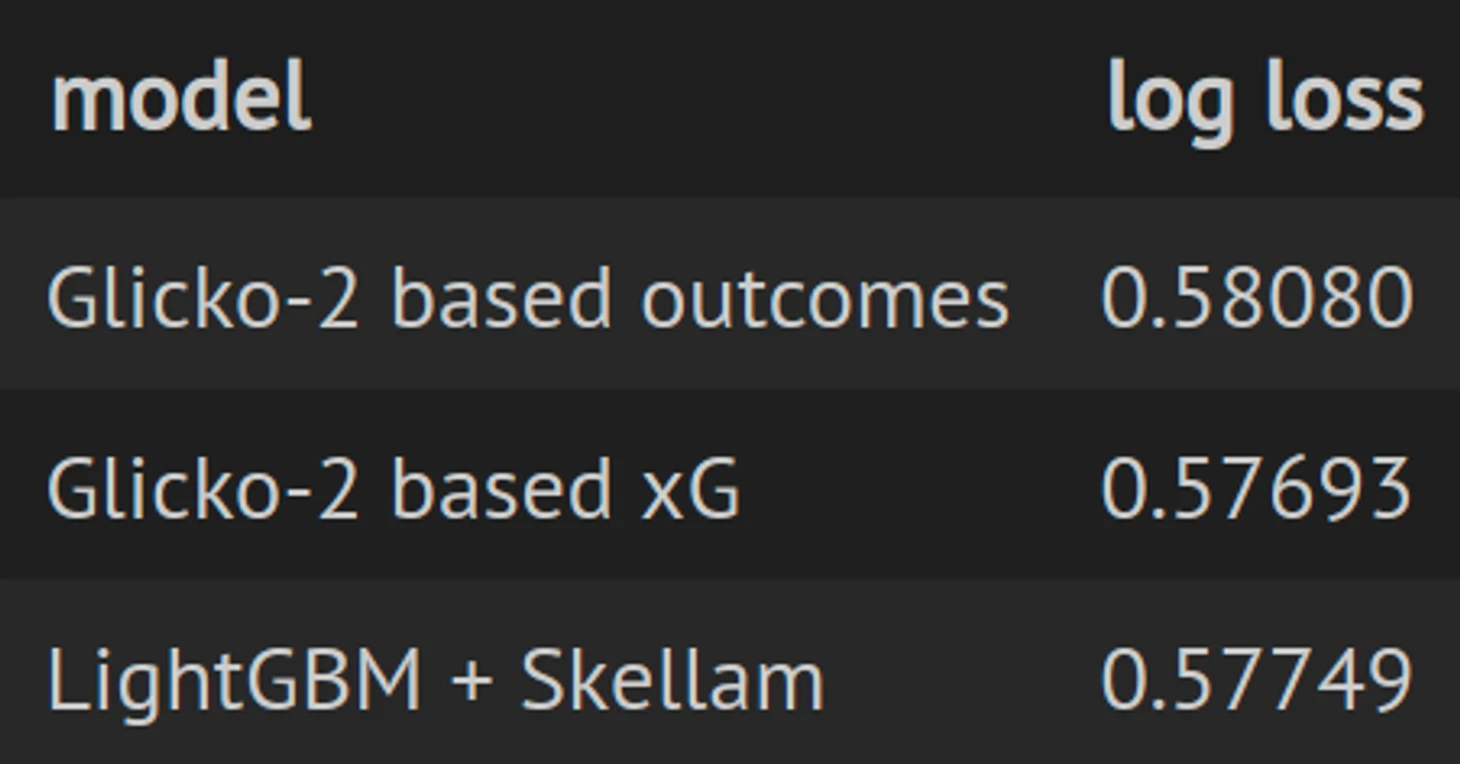
Лучшие результаты показал Glicko-2 обученный на данных по xG.
Получается, что мы зря старались, обучая LightGBM? Нет. Мы можем усреднить результаты моделей, возможно, это даст прирост точности. Только усреднять будем взвешенно: w1 * p1 + w2 * p2 + w3 * p3, где p1, p2, p3 – прогнозы моделей, а w1, w2, w3 – веса, который надо подобрать, при условии, что w1 + w2 + w3 = 1.
Подобрав веса, получили следующие результаты: w1 = 0.203, w2 = 0.46, w3 = 0.337, которые показали log loss 0.5731, что лучше каждой модели по отдельности.
Влияние пандемии на преимущество домашнего поля
Одной из проблем машинного обучения является то, что модели строятся в предположении, что исторические и будущие данные распределены примерно одинаково. Мы обучаем модель на старых данных, что-то предсказываем на новых и надеемся, что все будет хорошо. Часто на практике все бывает сложнее. Нассим Талеб называл такую проблему «проблемой индюшки». Мясник заботливо кормит птицу, каждый день у нее укрепляется убеждение, что человек хорошо к ней относится, ведь исторические данные не дают нам повода предполагать обратное. Потом наступает День благодарения и индюшка попадает на праздничный стол.
У нас похожая ситуация. Мы можем обучить параметр преимущества домашнего поля на трех предыдущих сезонах. На их основе сделать прогноз на текущий сезон. Но это будет неправильно, так как отсутствие болельщков повлияло на этот фактор.
Можно вообще убрать этот параметр: нет болельщиков – нет преимущества. Но дома играть проще не только по причине фанатов, которые поддерживают своих игроков, давят на чужих и на судью. Другой причиной является дискомфорт, связанный с переездом/перелетом в другой город. Например, The Athletic писал об ощутимом преимуществе «островных» команд.
Давайте посмотрим на данные
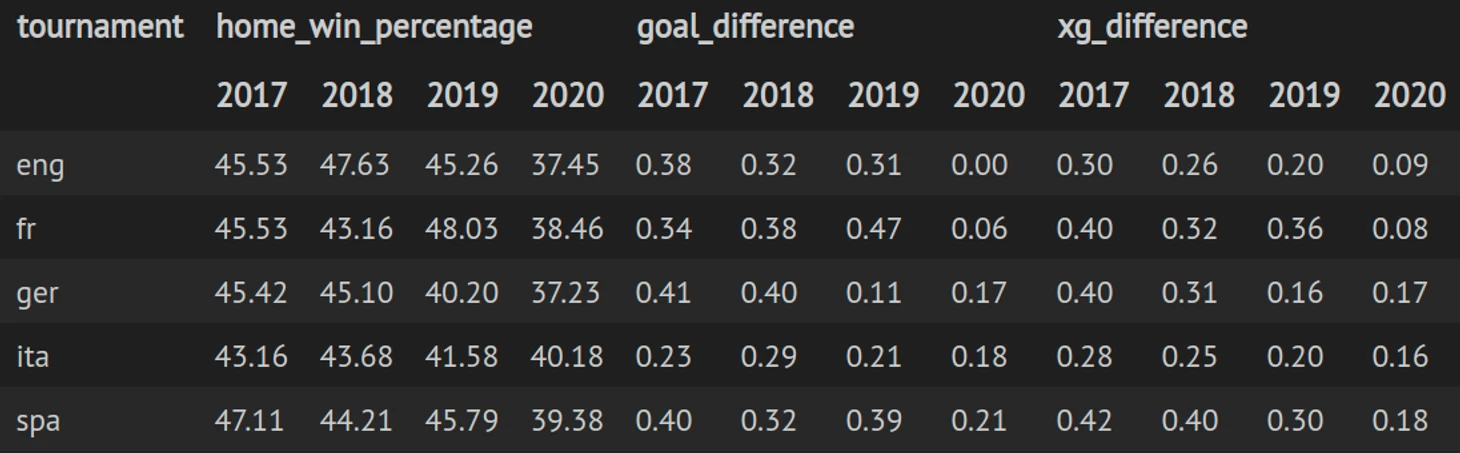
Видим, что в текущем сезоне во всех чемпионатах просел процент побед домашней команды, а также средняя разница в счете и в xG относительно хозяев поля.
В общем, подбирать параметр преимущества домашнего поля будем только на данных текущего сезона.
Прогноз будущих матчей
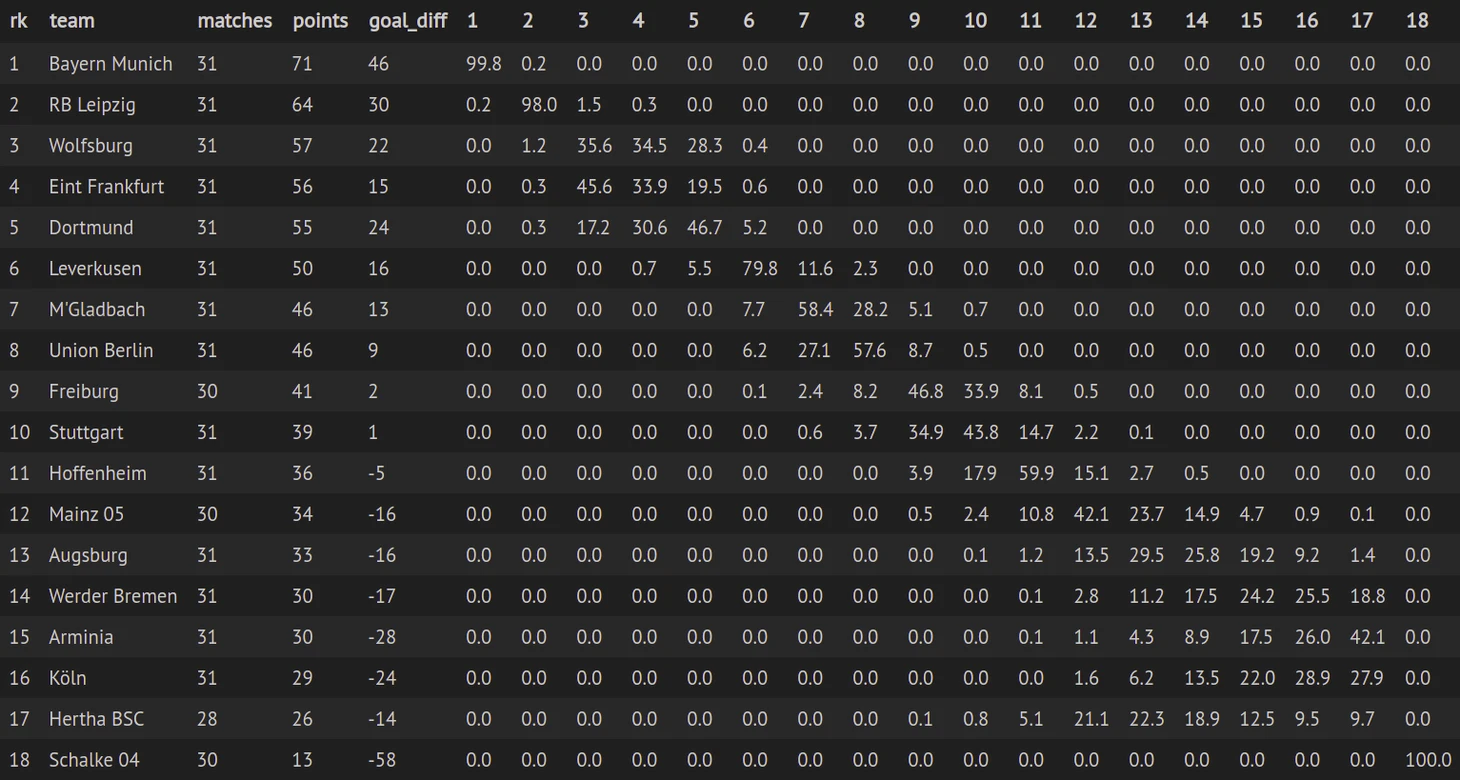
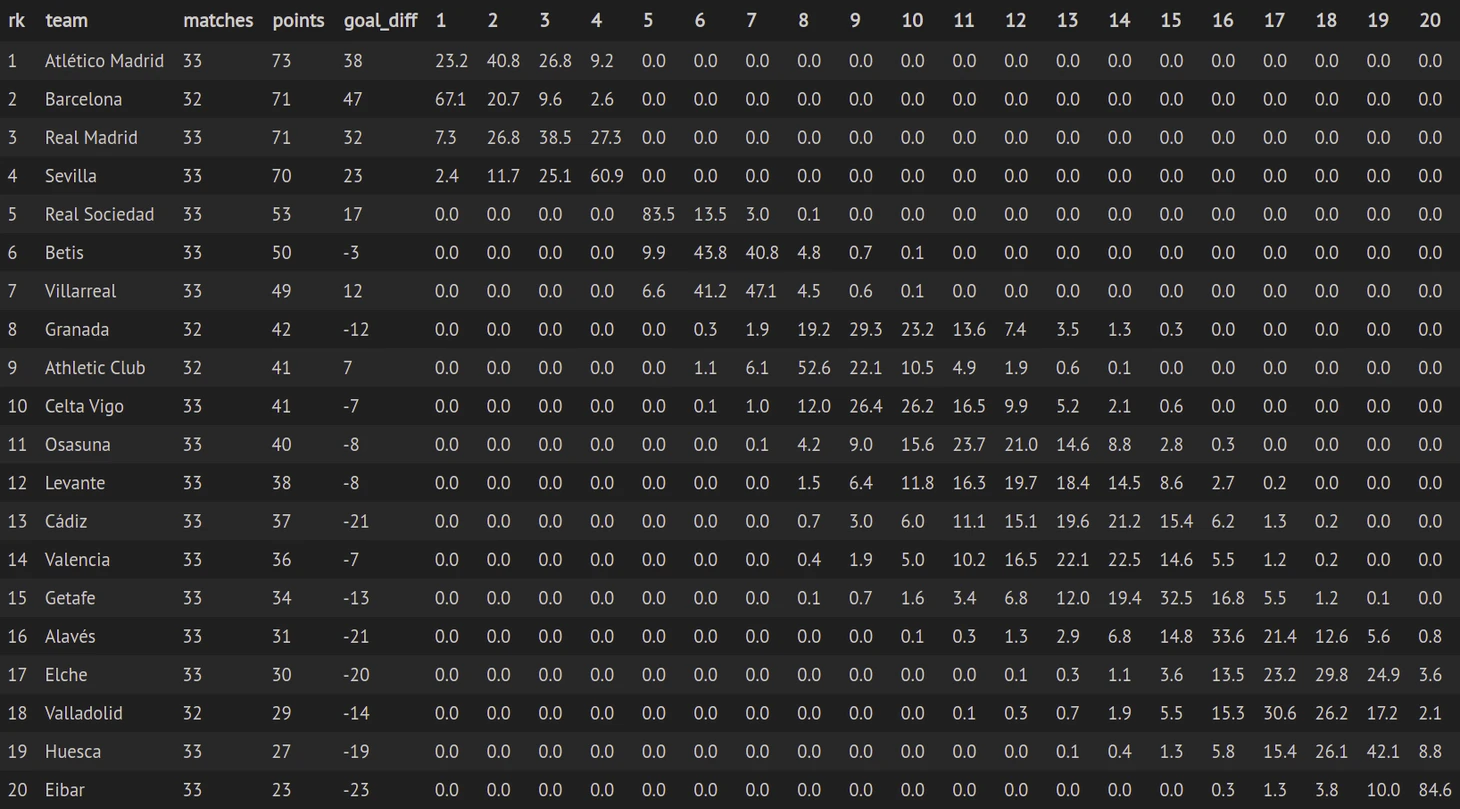
У нас есть прогнозы на будущие матчи, на которых запускаем метод Монте-Карло. Генерируем случайное число от 0 до 1. Если это число меньше вероятности победы, то засчитываем команде победу, если больше вероятности победы и меньше суммы вероятностей победы и ничьи, засчитываем ничью, в случае если случайное число превышает сумму вероятностей победы и ничьи, то поражение. Повторяем этот процесс 50 000 раз и считаем, сколько раз команда заняла каждое из мест. В результате мы получим вероятность занять определенное место для каждой из команд.
Давайте посмотрим, что получилось. В ячейках вероятности в процентах занять командой (строки) определенное место (столбцы).
Дата обновления 27.04.2021 10:00.
Англия
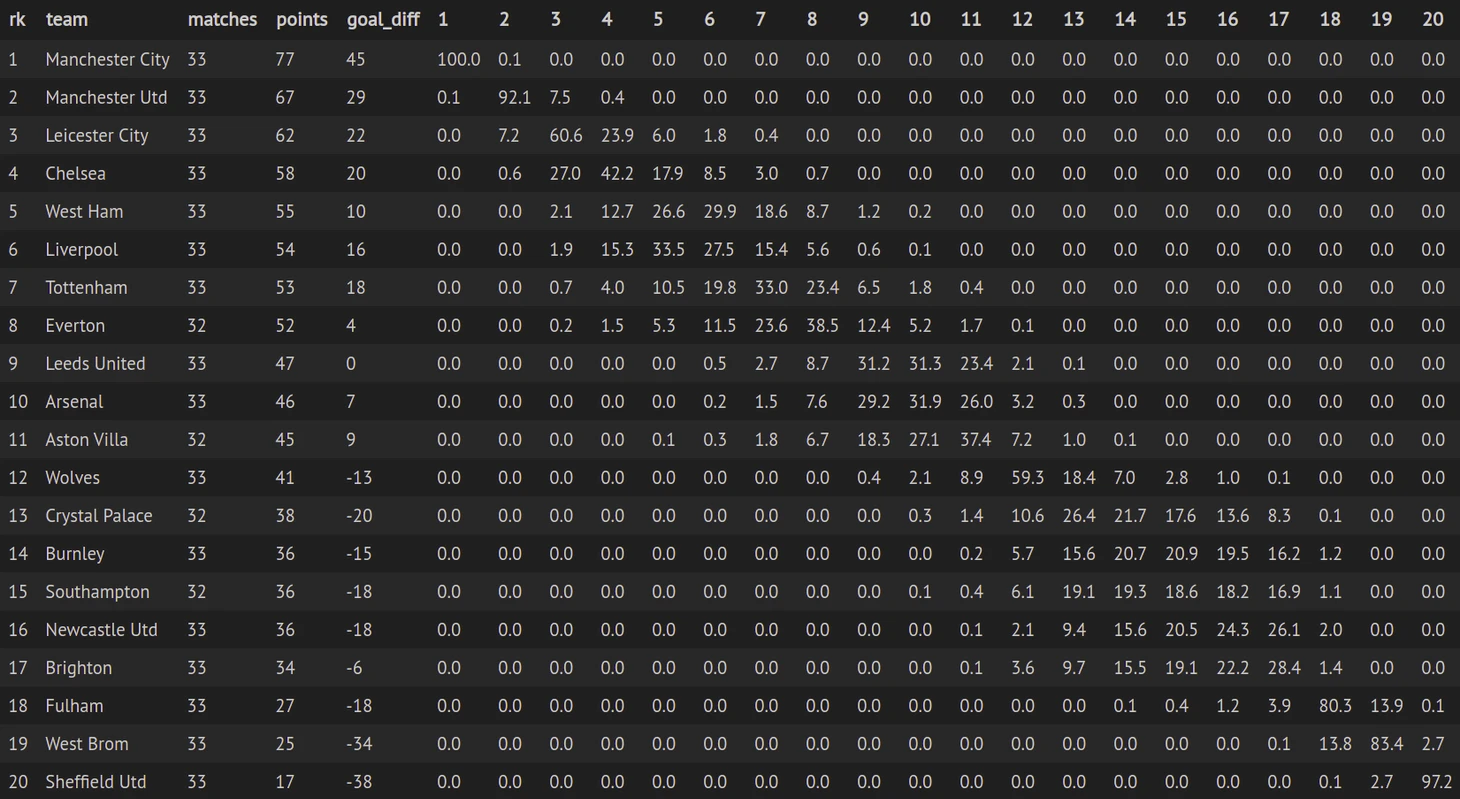
Германия
Испания
Италия
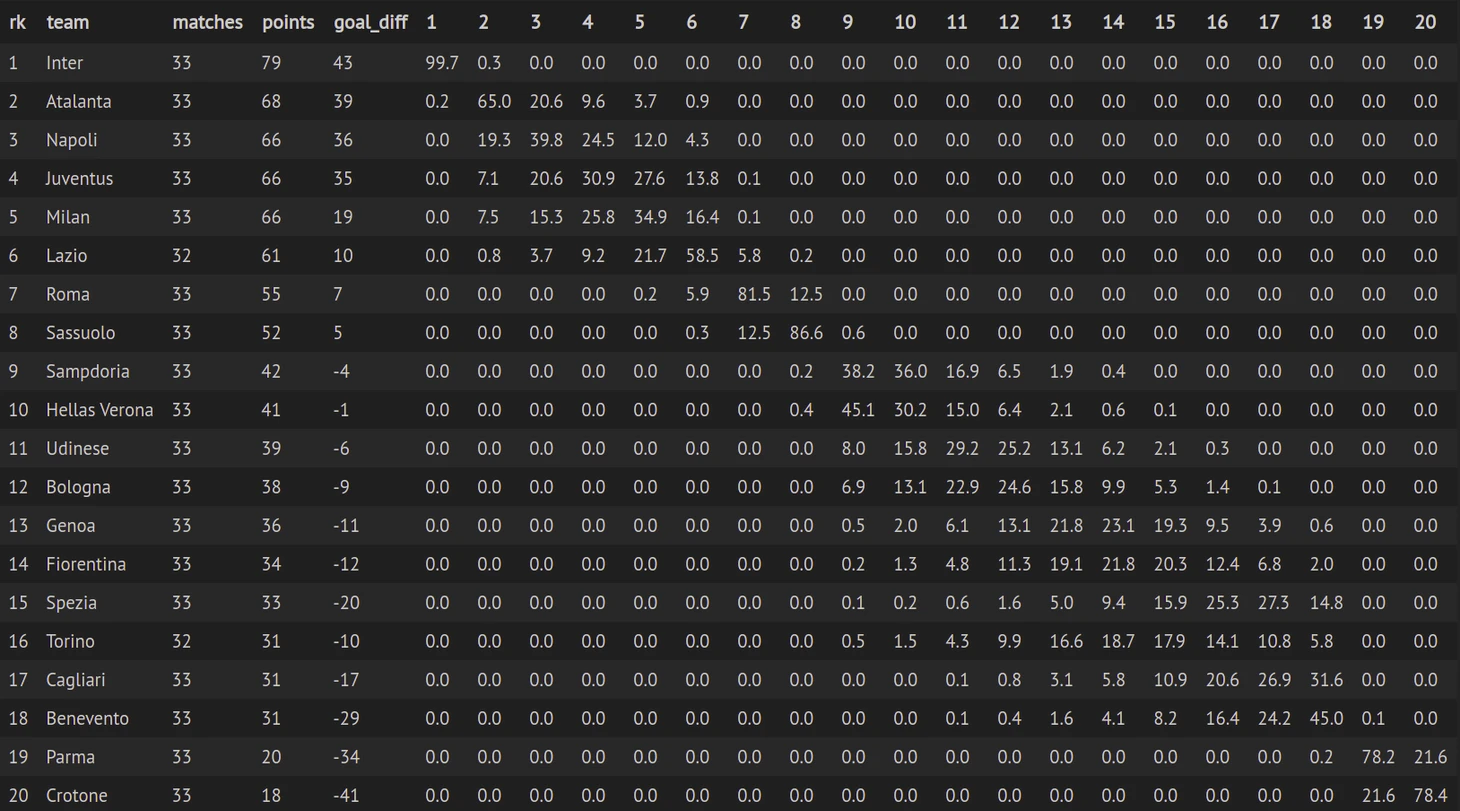
Франция
О системе в три очка
О природе случайности футбола написана не одна статья. Хорошее качество игры не всегда переходит в результат. Однако проблема закономерности результата заложена в самих правилах футбола. Раньше за победу давали два очка, за ничью одно, за поражение ноль. Это логично, команды разыгрывают награду, победитель забирает все, а в случае ничьи награда делится пополам.
Текущая система повышает зрелищность, но вредит справедливости. Она создает ассиметрию, где обмен победами 2:0 в двух кругах чемпионата оценивается выше, чем обмен ничьими 1:1. Три очка вместо двух, хотя даже общий счет одинаковый.
***
Также рекоменую прочитать статью Дэвида Шихана. Автор реализует модель Диксона-Коулса, которая решает проблему недооценки вероятности счета 0:0 и немного по-другому предсказывает количество забитых голов.
Кроме того, даже если предположить, что вы на самом деле считаете лучше букмекера, он рано или поздно просто заблокирует ваш счет.
Так что успехов конечно, но я никому бы не советовал даже пытаться. 99%, что ничего не выйдет.
По факторам, xG лучше предсказывает будущие результаты, чем голы. Фактор домашнего поля (в период пандемии) играет совсем небольшую роль.
Матч команд в первом круге и матч во втором — это ведь не связанные вещи. У команд травмы, смены тренеров, покупки, продажи, разная физическая форма, разные турнирные положения на момент матча и разыне турнирные задачи.
Сравнивать эти два матча — это такое себе вообще.
Это примерно как любят вспоминать перед матчами историю встреч команд за 30 предудыщих лет. Или за сто лет. Какая разница в чью там пользу сейчас соотношение, если к сегодняшней игре это не имеет отношения.