Предсказуемость футбола заложена в его природе. Проверяем на всех ведущих европейских чемпионатах
В прошлой статье я упоминал Дэвида Самптера и его книгу Soccermatics, которая на русском языке называется “Футболоматика: как благодаря математике "Барселона" выигрывает, Роналду забивает, а букмекеры зарабатывают состояния”. Название выглядит довольно провокационным, но все же автору удается в довольно легкой и увлекательной манере продемонстрировать читателям глубокое переплетение мира футбола и математики и по-новому взглянуть на всеми нами любимую игру.
Сегодня я предлагаю вам рассмотреть один из самых простых и в тоже время довольно эффективных способов прогнозирования в футболе, который освещается в первой главе упомянутой выше книги, и продемонстрировать его работу на данных, в которых отражена общая статистика результатов игр в ведущих футбольных лигах.
Ну что, поехали.
В первой главе своей книги Дэвид анализирует результаты Английской Премьер-лиги сезона 2012-2013 и вспоминает ряд матчей, результаты которых, как может показаться, демонстрируют нам непредсказуемость футбола.
Тот сезон запомнился великолепными матчами и неожиданными исходами – Ливерпуль дважды побеждал со счетом 5 - 0, один раз 6 – 0, но в итоге не смог попасть в еврокубковую квалификацию.
Сезон закачивался выходом на пенсию Сэра Алекса, под руководством которого Юнайтед в последнем туре чемпионата разошелся ничьей в гостях с Вест Бромвичем 5 – 5 в безумном матче с драматической концовкой, в которой хозяева отыграли 3 мяча за последние 10 минут. “Football — Bloody Hell!” – как однажды выразился Фергюсон.
Еще в одном матче того сезона было забито 10 голов – Арсенал дома победил Ньюкасл со счетом 7 – 3. Несмотря на то, что такие матчи болельщиками запоминаются сильнее всего, они являются исключениями и происходят не так часто в футболе.
В том же сезоне 2012-2013 было изрядное количество скучных ничьих 0 – 0, забытых фанатами, но не статистиками, в роли которого выступает сам автор и предлагает нашему вниманию 2 графика.

На первом графике результаты всех матчей того сезона отображаются в виде гистограммы, на которой по горизонтальной оси (ось x) находятся отметки, которые соответствуют общему количеству голов за один матч, а на вертикальной (ось y) представлено число матчей, в которых было забито соответствующее количество голов.
В сезоне 2012-2013 средняя результативность была примерно 2.79 голов за матч. На гистограмме мы можем наблюдать, что в том сезоне было 35 ничьих 0 – 0 (первый столбец гистограммы). Драматический матч Вест Бромвича и МЮ вместе с матчем Арсенала против Ньюкасла, в которых было забито по 10 голов, представлены последним столбцом гистограммы.
На середине гистограммы можно наблюдать самый высокий столбец, который говорит нам о том, что чаще всего в том сезоне команды забивали 3 гола на двоих (причем самый частый исход был 2-1). Данное отображение уже помогает нам увидеть некоторую закономерность и качественно оценить частоту тех или иных исходов, относительно общего количества голов за матч.
Следующим шагом мы попытаемся разобраться с тем, чем обусловлено именно такое распределение голов, и именно здесь к нам на помощь приходит математика.
Футбольный матч можно рассматривать как 90 одноминутных слотов, вероятность забить гол в каждый из которых одинаковая. Если взять среднее число голов за матч в рассматриваемом сезоне – 2.79, то можно определить вероятность забить гол в каждую минуту матча как 2.79 / 90 = 0.031.
Кажется, что это не очень большая вероятность, но нам достаточно и ее, чтобы с увлечением продолжать смотреть футбольную игру в предвкушении гола. В математической статистике есть инструмент, который позволяет нам зная одну только эту вероятность (вероятность гола в каждую отдельную минуту) определить то, как будет выглядеть итоговое распределение голов. Данный инструмент называется – распределение Пуассона.
Если очень просто, то это функция, которую можно применять для предсказания различных случайных событий окружающего мира, в том числе ее можно применять в футболе для вычисления вероятности того, что в матче будет забито определенное число голов. Зная эту вероятность и зная общее число матчей в течение сезона, можно также спрогнозировать итоговое число матчей, в течение которых будет забито соответствующее число голов.
Получаемые предсказания очень хорошо согласуются с реальностью, что мы видим на втором графике справа, где поверх исходной гистограммы голов наложено распределение Пуассона, полученное только на основе одного значения – 2.79 голов за матч.
Парадокс заключается в том, что все многообразие процессов, окружающих футбольное действо, начиная от подсказок тренера с бровки и радостного пения или гневных криков фанатов, заканчивая мыслями в головах игроков в решающие моменты футбольных матчей, не оказывает значительного эффекта на итоговое распределение голов в конце сезона. Даже наоборот, все эти факторы вместе создают тот элемент случайности, который позволяет этой модели работать.
Т.е. как бы это странно не звучало, чем больше факторов, вносящих элемент случайности, вовлечено в футбольный матч, тем более высока случайность гола и тем лучше будет работать распределение Пуассона и тем ближе будет прогноз к реальным результатам.
Несмотря на то, что приведенные выше тезисы могут показаться несколько странными и нелогичными, все букмекерские конторы хорошо знают эту особенность футбола и успешно пользуются этим знанием на регулярной основе.
В более строгом определении распределение Пуассона имеет ряд ограничений – оно может использоваться только для таких случайных событий, которые никак не связанны во времени, что вполне укладывается в то, что мы наблюдаем в футболе (если гол был забит на 2 минуте, то это никак не связанно с тем, на какой минуте в матче будет забит следующий и будет ли забит вовсе).
Подытоживая, хочется повторить, что абсолютно случайное событие – такое как гол в футбольном матче, имеющие одинаковую вероятность произойти для каждой конкретной минуты матча (т.е. каждая минута матча непредсказуема с точки зрения оценки вероятности забить гол), может быть предсказано с помощью распределения Пуассона. Получается, что природа самой закономерности находится в чистой случайности.
На этом моменте хватит о тонкостях и парадоксах распределения Пуассона, надеюсь вы еще не устали, т.к. сейчас начнется самое интересное, мы проверим, не вешают ли нам лапшу на уши и действительно ли так хорошо это распределение как о нем говорят.
В первую очередь попробуем реализовать самостоятельно приведенный автором пример. Идем на сайт football-data, качаем статистику за 2012-2013 год чемпионата Англии, строим гистограмму, считаем среднее количество голов за матч, строим поверх гистограммы распределение Пуассона и смотрим, что получилось.

Вроде бы все сходится, результаты автора удалось воспроизвести. Давайте теперь посмотрим чуть подробнее на последние 5 сезонов АПЛ и рассмотрим картину по текущему сезону. Для этого по аналогии построим фактическое распределение голов для каждого сезона, рассчитаем среднее количество голов за матч, построим распределение Пуассона и оценим, как часто полученная модель ошибается. В статистике качество модели оценивают с помощью специальных критериев, мы же просто посчитаем количество неверно определенных матчей.
Английская Премьер-лига в период 2015 - 2021
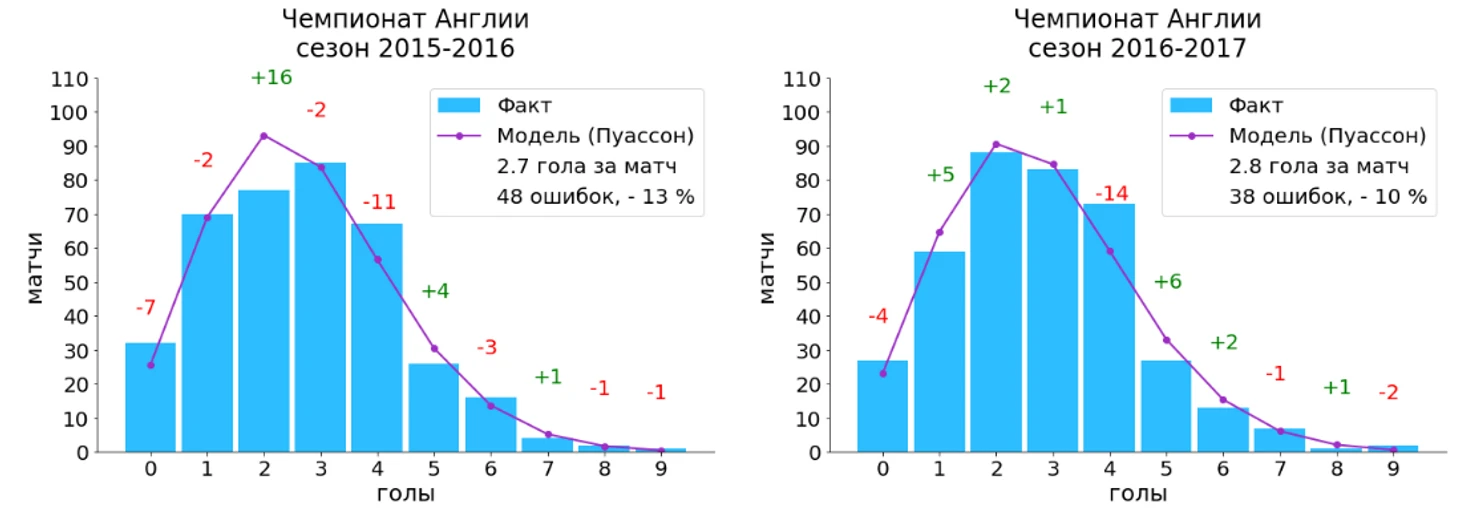
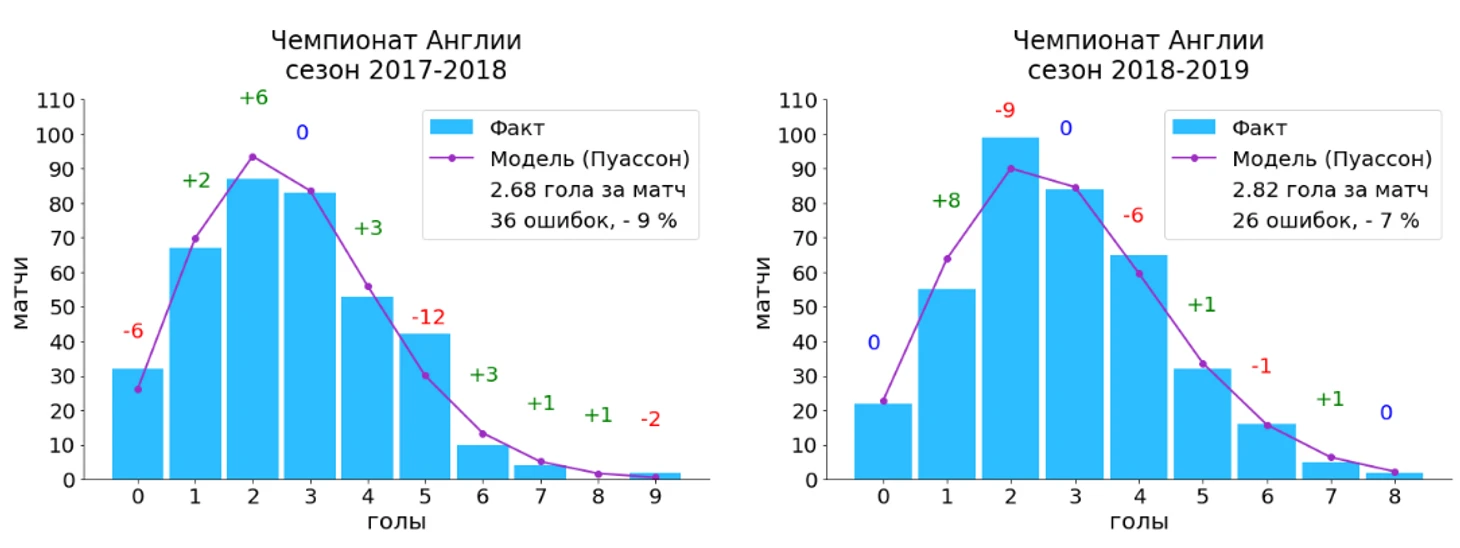
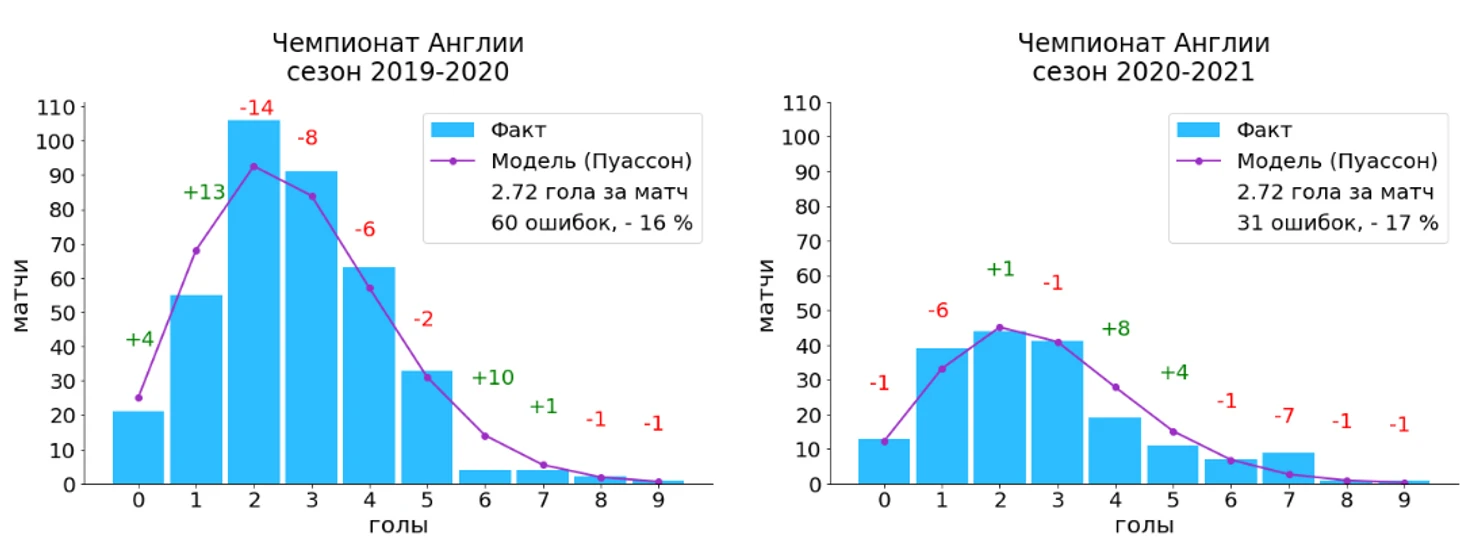
Мы можем наблюдать, что в целом из сезона в сезон общий вид фактического распределения забитых голов сохраняется. Только для сезона 2015-2016 наблюдается преобладание матчей с 3 забитыми голами, для остальных завершенных сезонов пик гистограммы соответствует 2 голам. Разница между моделью, полученной на основе распределения Пуассона, и фактическими результатами отражается в виде чисел над столбцами гистограммы, причем, положительное число указывает на то, что модель предсказывает больше матчей с соответствующим количеством голов, а отрицательное – наоборот, то, что в действительности таких исходов оказалось больше.
Мы можем наблюдать, что за 5 полноценных сезонов распределение Пуассона ошибается в диапазоне от 7 до 16 % от общего числа всех матчей (380 матчей за сезон). Выглядит впечатляюще, если учесть, что данный инструмент является одним из самых простых, используемых для прогнозирования, и что в нем используется только лишь один параметр – среднее количество голов. На последнем графике можно наблюдать текущую картину распределения голов в АПЛ.
Но быть может дело в самой АПЛ, и в других чемпионатах работают другие закономерности. Это легко проверить. Давайте теперь рассмотрим для каждой из топ европейских лиг аналогичные графики по прошлому сезону и картину для текущего сезона.
Европейские топ-лиги сезона 2019 - 2020 и текущий сезон 2020 - 2021
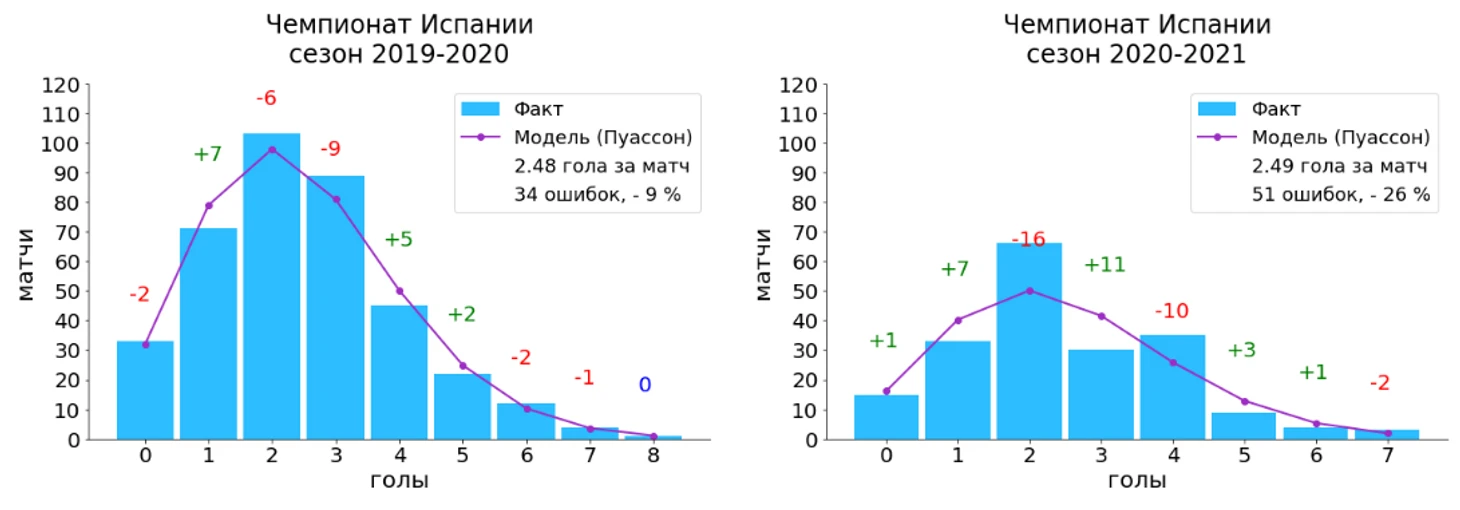
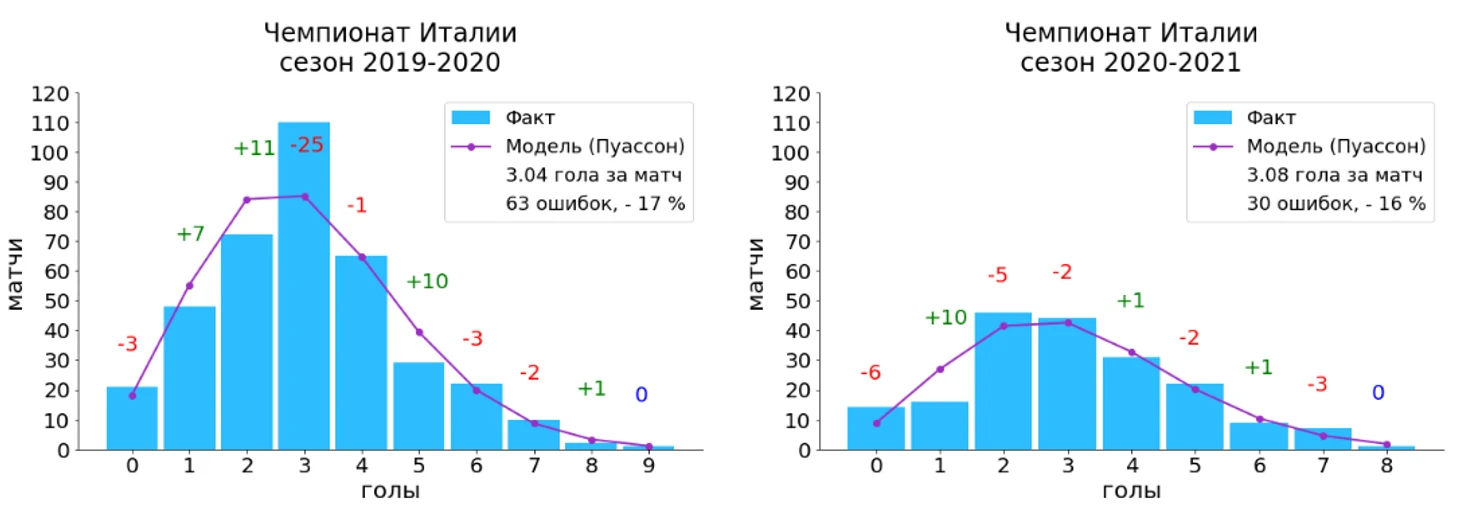
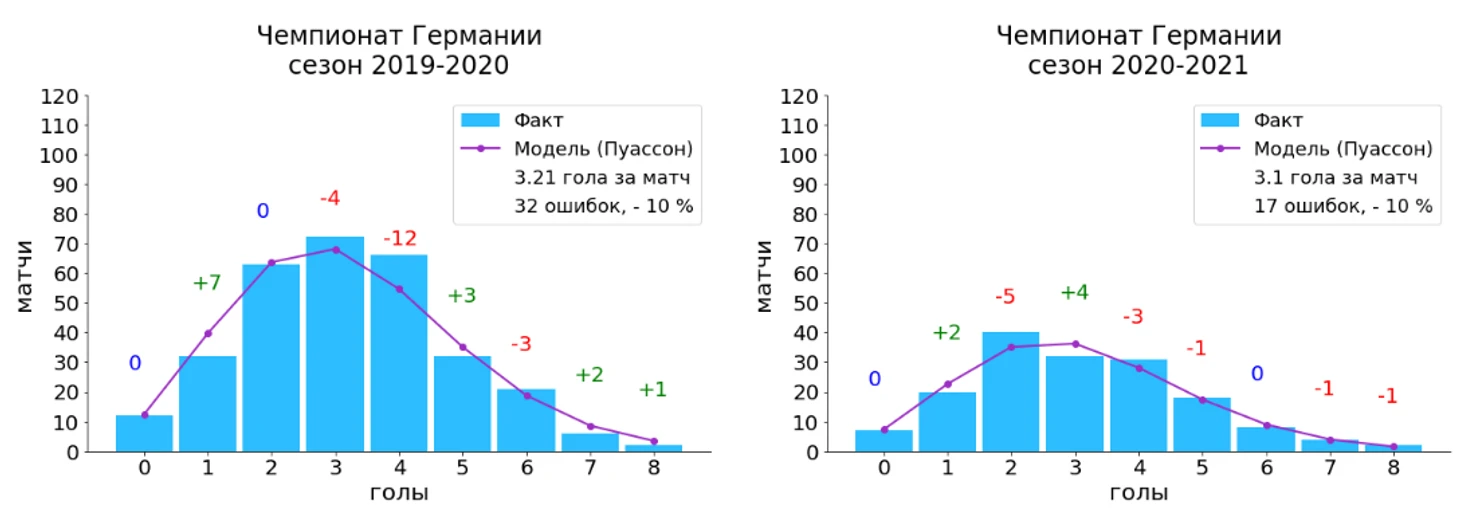
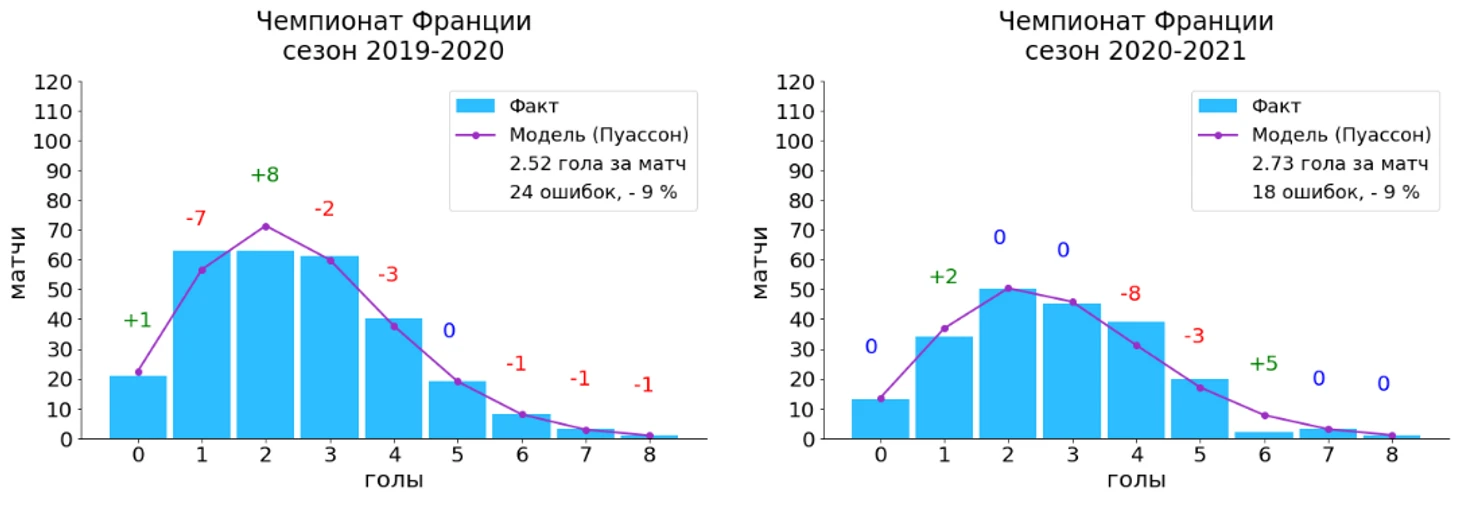
Стоит отметить, что при увеличении среднего числа голов за матч пик распределения Пуассона смещается в сторону большего числа голов (в сторону середины гистограммы), что мы можем наблюдать для лиг, в которых среднее число голов начинает превышать 3 гола за игру.
Если рассматривать прошлогодние сезоны, то можно отметить, что для чемпионата Испании мы наблюдаем картину, которая очень похожа на распределения голов в чемпионате Англии. Для чемпионата Италии и Германии мы видим, что среднее количество голов за матч начинает увеличиваться, и, как следствие, фактическое распределение и модель на основе распределения Пуассона начинают смещаться ближе к середине гистограммы.
Распределение для чемпионата Франции отличается сильнее всего от остальных, но это обусловлено в первую очередь тем, что чемпионат Франции не был доигран в прошлом сезоне и состоял из меньшего числа матчей, чем чемпионаты других стран (279 матчей в чемпионате Франции, 306 матчей в чемпионате Германии и по 380 в Испании и Италии).
Но самое главное, что несмотря на различия футбола в упомянутых лигах, несмотря на пандемию и множество других деталей, которыми были наполнены футбольные сезоны во всех рассмотренных чемпионатах, распределение Пуассона продолжает работать и довольно хорошо согласуется с реальными результатами (если смотреть на завершенные сезоны, то число ошибок модели не превышает 17% от общего числа матчей).
Безусловно, приведенные графики не позволяют вам делать предсказания итогового счета на конкретные матчи или расположения команд в турнирной таблице в конце сезона, основная задача данной статьи – продемонстрировать принципиальную возможность предсказаний в футболе, которая заложена в специфике природы самого процесса, с помощью довольно простого инструмента - математической статистики.
Но стоит отметить, что распределение Пуассона позволяет не только оценить распределение голов к концу сезона, оно также решает первые две упомянутые задачи. Если к данной теме будет проявлен значительный интерес у читателей, то я покажу, как данный инструмент используется в том числе для решения обозначенных задач.
Шаг 2












Прикладная польза заключается в том, что данные по прошлому сезону (нескольким сезонам) вы можете использовать, чтобы предсказывать результаты следующего сезона.
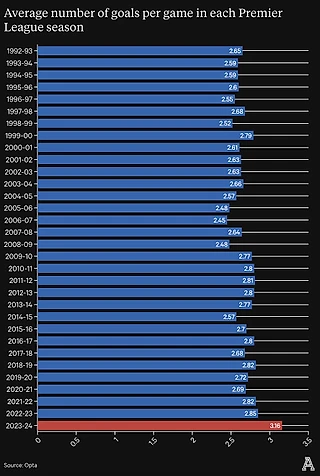
На примере с Англией в статье можно наблюдать, что общее среднее количество голов от года к году конечно меняется, но не сильно. Т.е. когда сезон только начинается, то вы опираетесь только на статистику прошлого года (на среднее прошлого года), чтобы предсказывать голы в текущем сезоне.
По мере течения сезона на основе вновь набираемой статистики можно вносить некоторые корректировки и пытаться в том числе предсказывать как изменится к концу сезона среднее количество голов, которое вы, в свою очередь, используете для предсказывания общего распределения голов. (т.е. вы не весь новый сезон используете среднее по прошлому году для предсказаний, а постепенно его корректируете).
Ну и прикладная польза заключается не в предсказывании общего распределения голов, а в предсказывании исходов матчей. Для этого считается уже набор средних величин: среднее число забитых и среднее число пропущенных голов для каждой из команд. При этом отдельно считаются такие средние для игр дома и игр в гостях.
На sports есть пример:
https://www.sports.ru/tribuna/blogs/foranol/717591.html
Или же аналогичный, только на Хабре:
https://habr.com/ru/post/318150/
В итоге, зная статистику по прошлому году (нескольким годам), с помощью Пуассона вы можете:
1. Делать предсказания (оценки) исходов матчей в новом сезоне
2. Делать предсказания расположения команд в итоговой турнирной таблице на конец нового сезона
2. Много думал об этом со вчерашнего дня и вроде бы понял. Грубо говоря, этот принцип может помочь в ставках, например: самая большая статистическая вероятность исхода матча должна давать больше шансов на выигрыш, поэтому если посмотреть на кэффы букмекеров, то, как правило, самые низкие предлагаются как раз на счет 1:0 и 2:1.
В целом, это и так интуитивно понятно, как мне кажется, но такое математическое подтверждение безусловно интересно.
Пример из другой сферы: у авиаперевозчиков и отельеров есть понятие "динамические тарифы" или "revenue menegment", главный принцип которого "продать услугу нужному человеку, по нужной цене, в нужное время", то есть в зависимости от спроса и других факторов цена на одну и ту же услугу может колебаться кратно: один и тот же номер в курортном отеле летом на выходные - 10000 рублей, во вторник в ноябре - 2000 рублей. Благодаря распределению Пуассона они могут точно понять в какой из дней недели/времени рейса моно установить максимальную цену, а когда минимальную. То же применимо и к кинотеатрам, радио и тв рекламе и еще много к чему.