Если долго ожидать
В последнее время я нередко слышал высказывания от знакомых, встречал материалы на Sports.ru относительно прогресса Бёрнли. Я всецело за аутсайдеров, выдающих неожиданные результаты на длинной дистанции. Но Бёрнли является исключением из этого списка. Позвольте объяснить почему.
Глава первая. Банальная статистика
Команда Дайча имеет только 44% владения и, следовательно, большую часть матча действует без мяча. Но если у тебя нет мяча, то подразумевается, что ты будешь забивать с контратак и/или со стандартов.
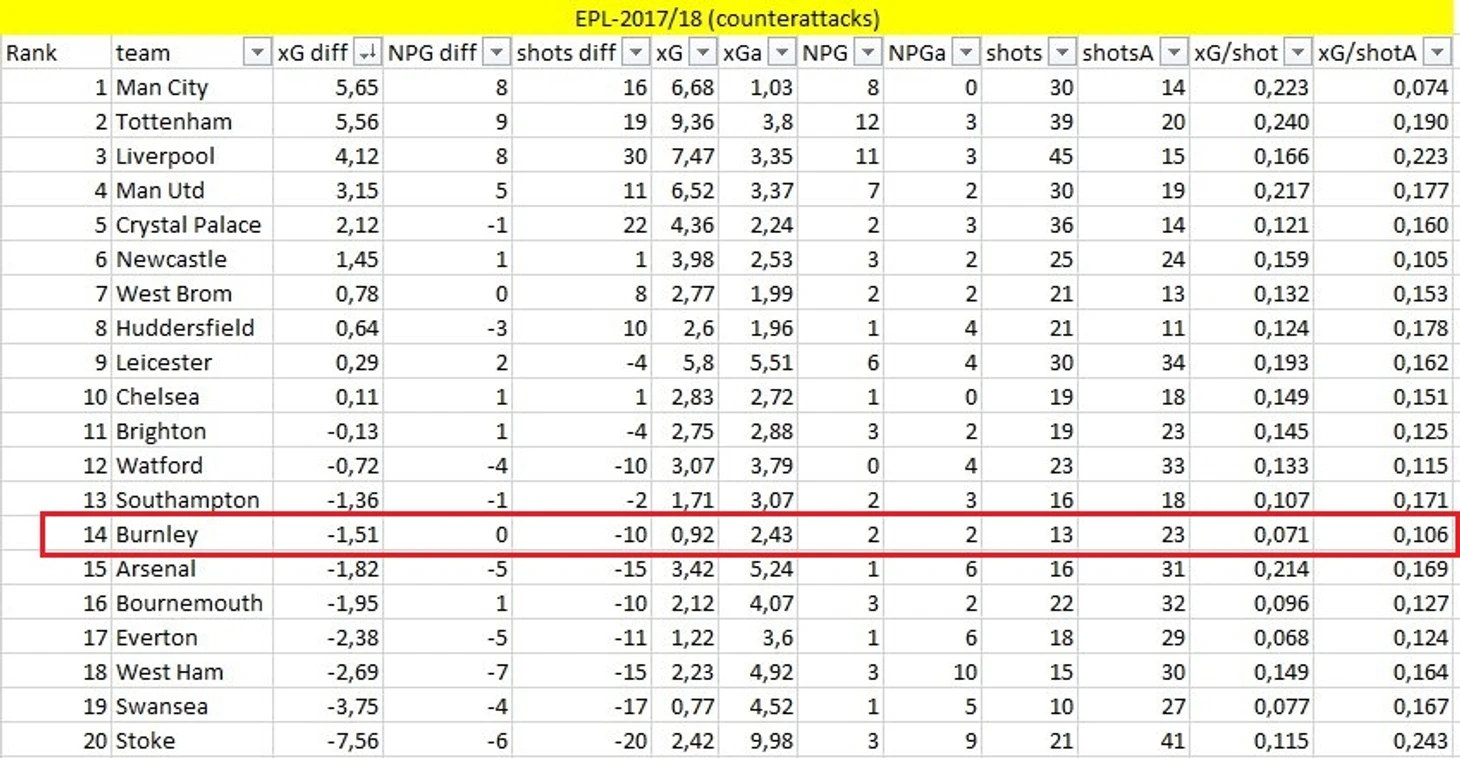
Выше представлена таблица контратак АПЛ. После своих контратак команда Дайша нанесла целых 13 ударов (второй с конца результат), суммарная опасность которых достигла 0,92 Xg (и это снова второй с конца результат; в обоих случаях хуже только совсем уж мёртвый Суонси). Да, Бёрнли не позволил много создать своим соперникам, но это, скорее, индивидуальные заслуги Тарковски и Мии, имеющих, к слову, лучшую среднюю оценку в команде. Вывод - Бёрнли не опасен при контратаках.
Теперь о стандартах. Ниже вы видите текущую таблицу стандартов АПЛ.
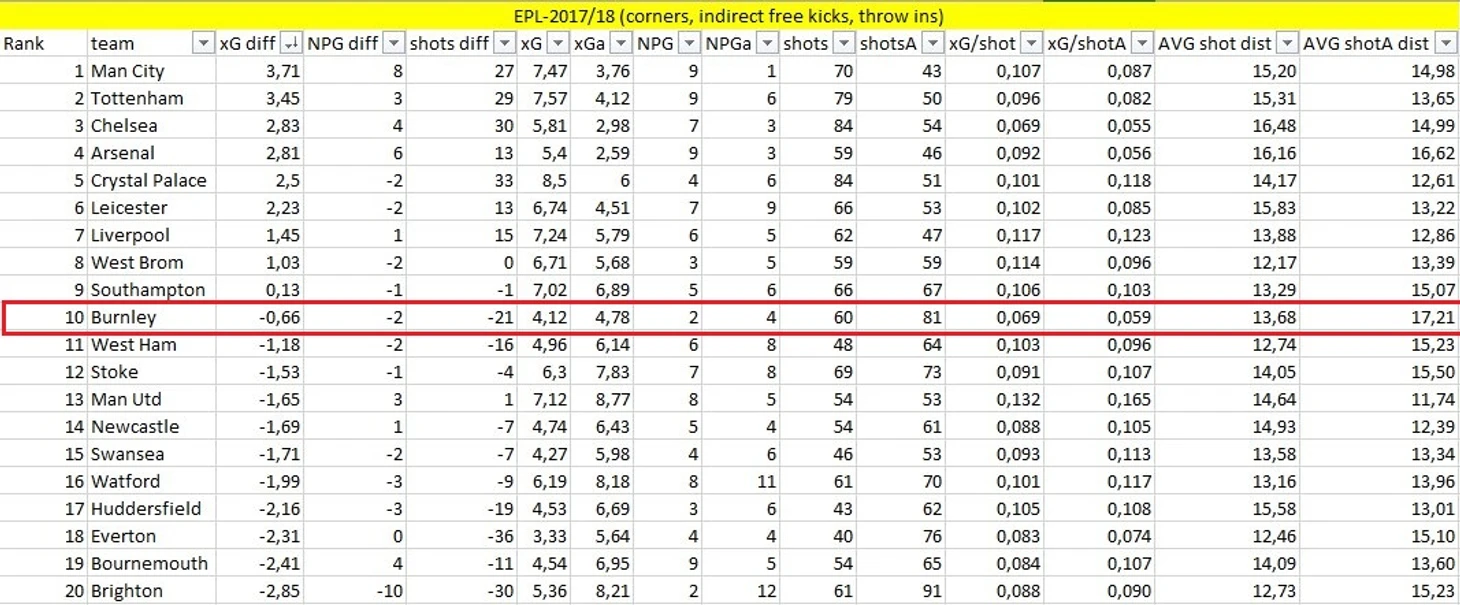
Ударов нанесено после стандартов - 60 - неплохой, прямо скажем, показатель.
xG этих ударов равен 4,12 - уже не так впечатляет.
Получается, далеко не все из этих 60 ударов представляли хоть какую-то опасность для соперника, и это подтверждается статистикой - xG/shot (среднее xG каждого удара) равен 0,069, что наравне с Челси является худшим показателем в лиге. Выходит, и со стандартов Бёрнли не представляет особой опасности.
Складывая 44% владения, вторые с конца контратаки и далеко не лучшие стандарты, мы получаем 0,8 гола в среднем за игру. Но прагматичность это не главная черта данной команды. Главная - удача. А как иначе можно объяснить набор "лишних" 13 очков? А ведь это более чем треть от общего количества очков, набранных Бёрнли, и без них, команда шла бы на 19-м месте
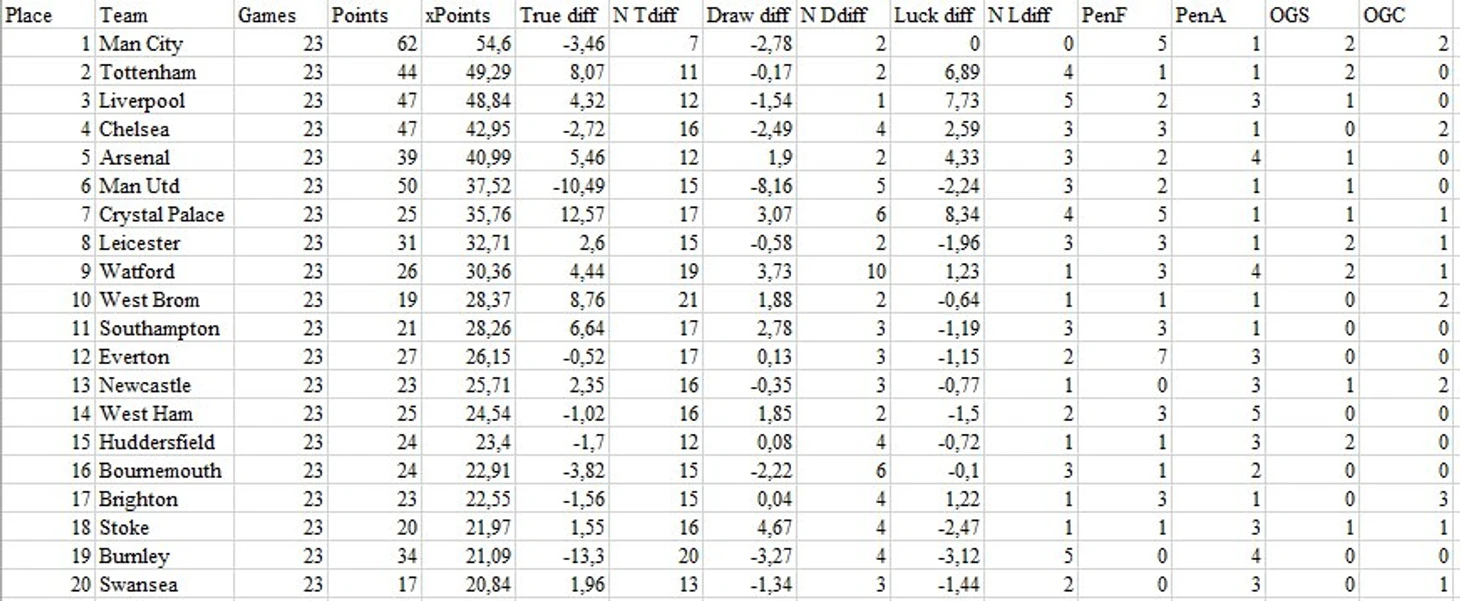
И почему лишь на 7-й год руководства Дайча Бёрнли "заиграл"? В этом я и попытаюсь разобраться.
Математическое объяснение.
Вы когда-нибудь задумывались о том, что случайные, на первый взгляд, события (такие как гол Чалханоглу в ворота Дортмунда с 45+ метров) на самом деле поддаются прогнозированию? Что если мы можем прогнозировать частоту (общую) случайных событий и вероятность того, что они произойдут? Да, мы не можем сказать когда именно произойдёт событие, но мы можем вполне точно предположить их общее количество, используя распределение Пуассона и теорему Якоба Бернулли. Пример:
Какова вероятность выпадения решки при подбрасывании монеты? 50%. То есть шансы выпадения или решки, или орла составляют 50/50.
Каков шанс выбросить восемь раз подряд решка? Крайне низок (1/256, если кому интересно). Но если заниматься этим на протяжении 40 лет - бросать друг за другом 8 монет по 4 раза в неделю, - то получится, что каждую из монет вы подбросили 8000 раз (или очень близко к этому). 8000 раз каждую, а всего их, напоминаю, восемь, то есть суммарно вы сделаете 64 000 вбрасываний. За этот период времени шанс увидеть восемь решек подряд возрастает многократно - вы практически наверняка выбросите восемь решек подряд.
Это я всё к чему. Суть теоремы Бернулли (также известной как Частный случай закона больших чисел по Бернулли) заключается в следующем - чем больше вы что-либо делаете, тем больше вероятность того, что вы встретите наименее популярный (=наиболее невероятный) результат из всех возможных вариантов. Соответственно, если вы давно в футболе (как, например, Шальке), то рано или поздно, вы отыграетесь со счёта 0:4 (как это было в матче с Дортмундом), ведь согласно закону в течение долгого периода времени всё, что угодно, может произойти хотя бы 1 раз.
В нашем случае роль решек, выпавших восемь раз подряд, выполняет серия Бёрнли, в течение которой они и перебрали эти 13 очков, выигрывая матчи, создав моментов буквально на 0,2 xG.
По такому же принципу отыгрался Ливерпуль в "стамбульском финале" (Ливерпуль давно занимается футболом, и, следовательно, рано или поздно они бы отыгрались с 3:0), по такому же принципу Арсенал остался непобеждённым в сезоне 2003/2004 (рано или поздно должна была хоть одна команда не проиграть ни единого матча в чемпионате).
Как видите, математика и вправду может объяснить фактор удачи в футболе, и если этот пост возымеет хорошую отдачу, я могу продолжить тему взаимосвязи математики и футбола.











