Почему хороший нападающий и хорошая реализация - совсем не одно и то же
Первая часть: “Влияет ли сила команды на реализацию моментов?”
Как правило, если игрок плохо реализует моменты, болельщики тут же записывают его в “бревна”, “деревья” и прочие лесоматериалы. Но действительно ли отношение реальных и ожидаемых голов определяет уровень игрока? При беглом взгляде кажется, что если футболист забивает лучше ожидаемого, его стоит признать сильным нападающим. А так ли это на самом деле? Может ли быть, что реализация является совершенно непредсказуемой величиной? Воспользуемся несложным математическим аппаратом для ответа на эти вопросы.
Итак, строго говоря, нам нужно выяснить две вещи:
Зависит ли реализация игрока в i-ый сезон от его реализации в (i - 1)-ый сезон?
Зависит ли реализация игрока от его класса?
В этом материале не будут использованы сложные средства, поэтому текст должен быть понятен и несвязанным с математикой людям.

Выборка и переменные
Были взяты данные по топ-6 лигам (Испания, Англия, Италия, Германия, Франция, Россия) за сезоны 14/15 и 15/16; фильтрация по игрокам, набравшим более 5 xG в каждый период. В выборку попало 129 игроков.
По-новому считается реализация игроков - если раньше бралось простое отношение числа реальных и ожидаемых голов NPG/xG, то сейчас считается натуральный логарифм этой величины: r = ln(NPG/xG). Простым языком, теперь распределение получается более симметричным. Если раньше “плохая” и “хорошая” реализации находились в неравных интервалах - (0; 1) и (1; +∞) соответственно, то теперь промежутки отличаются только знаками - (-∞; 0) и (0; +∞). Тесты показали лучшее соответствие нормальному распределению.
Характеристика уровня атакующих навыков игрока (иначе говоря, “класс” нападающего при условии, что единственная его задача - забивать голы) - xG/90, величина, показывающая, как часто игрок имеет моменты.
Реализация в последовательные сезоны
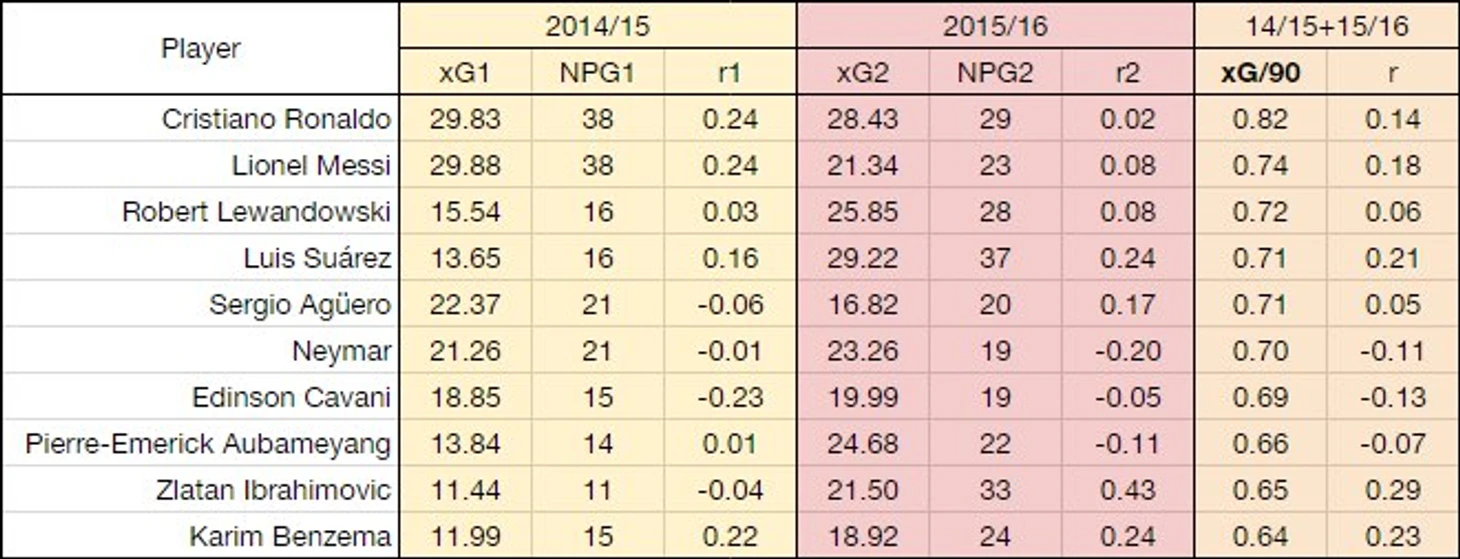
Реализация лучших по xG/90.
r1 и r2 - показатели реализации в два последовательных сезона - 14/15 и 15/16. R^2 между этими величинами равна 0,0004, что является очень низким значением. Это говорит о том, что никакой прямой связи между реализацией в два последовательных периода нет. Для сравнения, R^2 между xG/90 в сезонах 14/15 и 15/16 равен 0,38. Между NPG/90 - 0,22. К слову, это говорит о том, что xG/90 - лучший индикатор качества нападающего, чем NPG/90.
Небольшой ликбез: R^2 - это величина, показывающая степень зависимости одной величины от другой (других). Она принимает значения от 0 до 1. Для двух независимых друг от друга величин коэффициент будет равен нулю, для строгой линейной зависиости (y = kx + b) - единице.
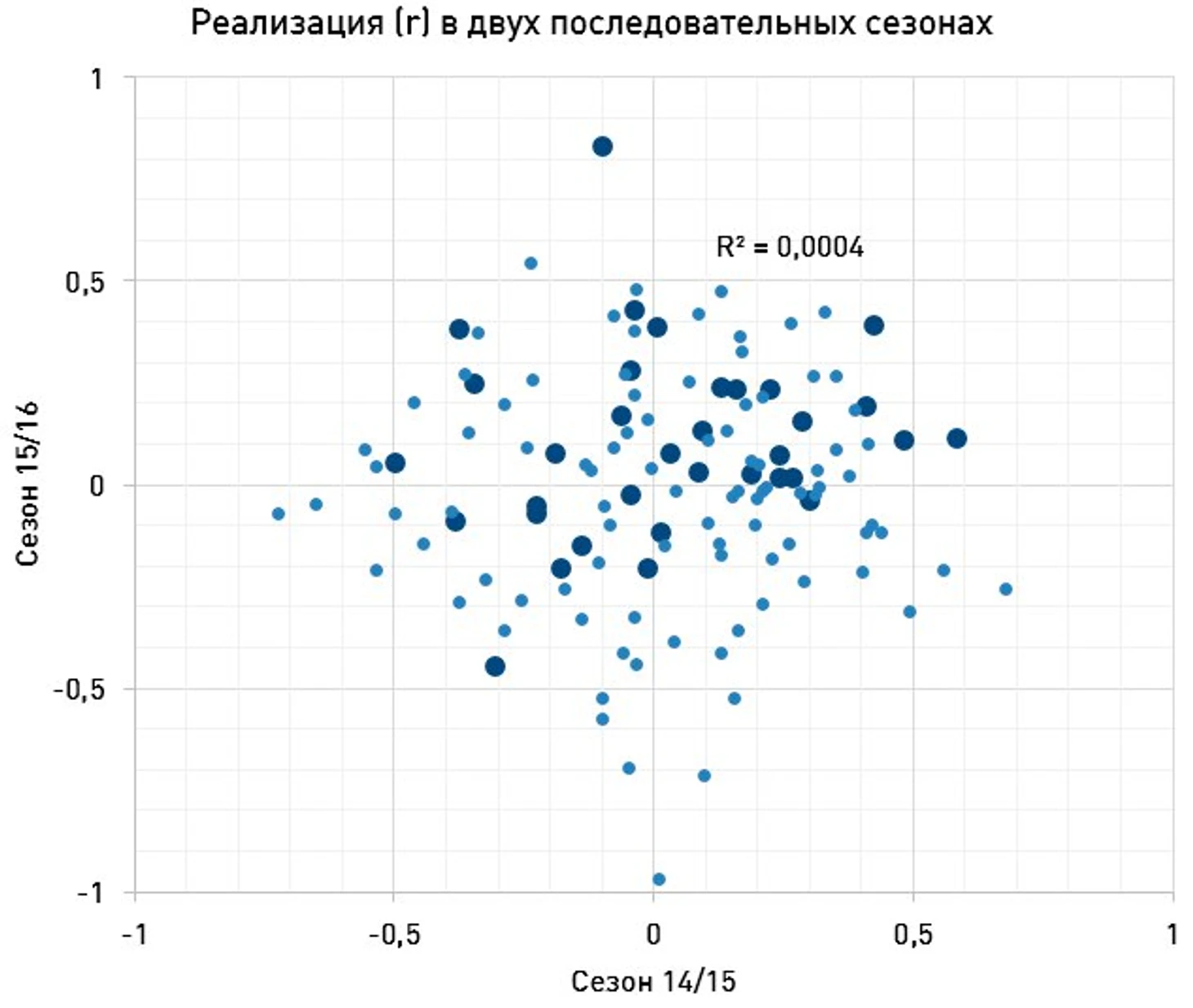
Более темные жирные точки - игроки, в каждый из сезонов имевшие больше 7 xG и в сумме за два - больше 20 xG. Можно говорить, что эти наблюдения более значимы.
Зависимость реализации от уровня игрока
Хотя реализация неповторяема, возможно, она положительно коррелирует с уровнем игроков. Кажется логичным предположение о том, что условный Агуэро будет реализовывать стабильно лучше Прудникова. Проверим это предположение:
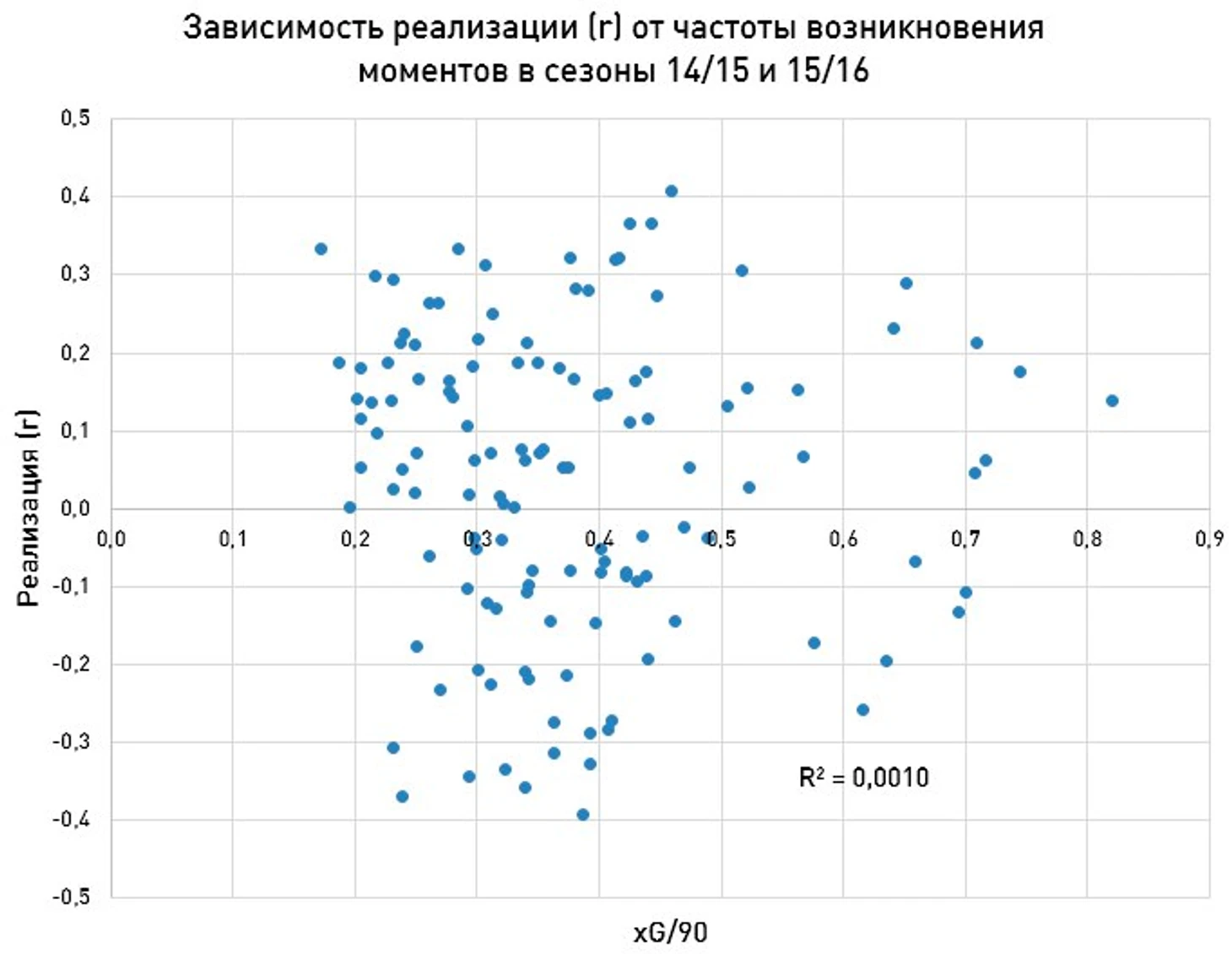
Налицо гетероскедастичность, что заставляет нас делать выводы с большей осторожностью.
R^2 между r и xG/90 равен 0,001, что является очень низким значением. Несмотря на неполное соответствие предпосылкам МНК, мы можем утверждать, что реализация не зависит от частоты возникновения моментов у игрока.
Выводы
Ответ на оба поставленных в начале текста вопроса оказался отрицательным. Итак:
Реализация игрока не зависит от аналогичной величины в предыдущем сезоне
Частота возникновения моментов не влияет на реализацию
Возможно, в отдельно взятых редких случаях игрок может сохранять реализацию моментов на стабильно высоком уровне из-за нестандартного стиля игры команды, но в целом, по реализации нельзя оценивать уровень игрока. Как уже было отмечено в англоязычных источниках, качество нападающего определяет количество моментов, а не их реализация.
Если рассуждать дальше, появляется вопрос - а нужно ли вообще игрокам, уже достигшим уровня топ-лиг, тренировать удар больше какого-то минимума? Но это тема для другого разговора, поскольку для уверенного ответа нужны исследования другого характера.
Спасибо за предоставленные данные Андрею Кривоногову и Wyscout, а за комментарии и замечания - Никите Васюхину и Евгению Михайлову.
Подписывайтесь на Блокнот, любите математику и помните о трех видах лжи.











тогда слишком сильно будет заметно насколько нап зависит от своих партнеров, условно говоря, играй Прудников за Манчестер Сити его реализация возрастет, так как и моментов у него будет создано больше?
а нельзя ли еще как нибудь разграничить ситуации когда нап сам себе создает момент за счет обыгрывания соперников или движения на острие под дальние и средние передачи, от тех, когда он просто удачно подставляет ногу или играет на добивании?
"Небольшой ликбез: R^2 - это величина, показывающая степень зависимости одной величины от другой (других)"
Нет, это величина, показывающая качество аппроксимации регрессионной модели.
Во-первых, для зависимости R используют, а не R^2 - Пирсоновский коэффициент корреляции.
Во-вторых, в вашем случае этот коэффициент оценивает обычный коэффициент корреляции, который показывает именно линейности зависимости. Например, у Х и Х^11 для нормальных данных он будет близок довольно маленьким, хотя они не просто зависимы, а зависимы прямой функциональной зависимости, нужный нам коэффициент должен быть 1.
Поэтому для изучения прямой зависимости используют ранговые коэффициенты, например, Спирмена или Кенделла, вот они как раз следят правда, ли что когда один параметр больше, то и второй больше.
Скорее всего итог при этом будет близкий, зависимость действительно не очень большая, это и визуально видно. А вот для тех, кто большими кружками отмечен, кажется, что зависимость есть и не такая уж маленькая.
Только вот есть вопрос - а это действительно тот самый показатель реализации, о котором обычно говорят болельщики? Скажем, если человек забил 9 из 10 выходов 1 в 1, то у него большой xG и много голов. Если он вместо этого бьет 10 раз издали (так, что удар стоит в десять меньше) и забивает 1 раз, то у него даже больше ’’реализация’’.
Другие выводы и вовсе не очень хорошие.
"Для сравнения, R^2 между xG/90 в сезонах 14/15 и 15/16 равен 0,38. Между NPG/90 - 0,22. К слову, это говорит о том, что xG/90 - лучший индикатор качества нападающего, чем NPG/90."
Нет, это просто значит, что они зависят "линейнее", то есть мы ближе к "год от года показатель реализации изменяется у игроков в одно и то же количество раз для всех игроков’’. Это какая-то странная характеристика качества индикатора.
К слову, этот коэффициент тоже считается только по тем, у кого хотя бы 5 xG?
А в следующей статье из этих рассуждений делается вывод "по ним лучше оценивать страйкера, чем по голам".
К этому моменту автор уже забыл, что он исследовал зависимость реализации, а вовсе не голов.
На большинство тезисов отвечу лишь, что это статья не в научном журнале, а на спортивном сайте, поэтому, полагаю, могу позволить себе жертвовать абсолютной точностью ради понятности не самому подготовленному читателю.
Тезис про разное понимание реализации отчасти кажется какой-то казуистикой. Конечно, модель не учитывает умения выбора позиции для удара и подобные параметры - это является серьезным недостатком. Но, думаю, обыватель будет понимать, что кроме реализации, существует умение выбора момента для удара, которое у второго игрока явно хромает.
Вывод про лучший индикатор качества, наверное, и правда не очень аккуратен. Но далее в материале это утверждение подтверждается. А R^2 для голов/90 считался по той же самой выборке, что и для xG/90.
Суть последней претензии я не понял - распишите, пожалуйста, подробнее.
Во-первых, как я уже говорил "линейная зависимость" это не то же, что "зависимость". Причин ожидать здесь именно линейную зависимость не видно, кажется логично искать именно монотонность.
Во-вторых, вы фильтруете данные по xG не меньше 5 в двух сезонах. После эти выводы распространяете на всех футболистов. Но это так не работает. Возьмите, например, X,X+Y, где X,Y независимы и равномерны на [0,1]. У них корреляция 0.7. А если вы возьмете ту долю, которая соответствует X>1/2, то она 0.4. Цензурирование по параметру меняет корреляцию.
Поэтому на самом деле постулировано "Реализация игрока не зависит от аналогичной величины в предыдущем сезоне", а доказано "Статистический показатель "реализация" для футболистов, поддерживающих xG больше 0.5 два сезона, реализация в эти сезоны если и будет зависима, то нелинейно".
Это
а) не запрещает любой другой зависимости (например, реализация у одних игроков падает, потому что они сдают, а у других растет, потому что они прогрессируют, это уже нелинейно).
(Судя по данным это малореально)
б) не запрещает тесной связи реализации в разные сезоны по всем игрокам, которая ослаблена рассмотрением только игроков с постоянно большим xG
в) не запрещает сильную зависимость реализации в разные сезоны у отдельных игроков, просто таких игроков не очень много. Он малопоказателен только для той совокупности, которую вы изучали - всех игроков с xG больше 5 за два сезона, а для какой-то ее подсовокупности может быть куда как более показательным.