5 мин.

Перес все купил!?

146

Последние годы мадридский Реал подозревают в подтасовках во время жеребьевок Лиги Чемпионов. Используя методы матстатистики, можно проверить, насколько редким будет выпадение столь слабых соперников при условии отсутствия внешнего влияния на исход жребия.

Методика

Суть метода состоит в следующем: вводится функция силы команды (далее, ФС). Затем, находятся значения ФС всех возможных соперников в рассматриваемых жеребьевках. В каждой отдельной жеребьевке команды сортируются по возрастанию ФС (самая слабая из доступных команд получает номер 1). Согласно позиции, но без учета ФС, рассчитывается рейтинг силы (далее, РС) потенциальных противников, принимающий значения со средним 0,5. После этого, находится выборочное среднее значение РС реально выпавших команд во всех жеребьевках и ищется квантиль распределения возможных средних РС, в который попало реальное значение этого параметра.

Описание выборки

Напомним регламент: на стадии 1/8 финала команда, занявшая первое место в группе, может попасть только на команду, ставшую второй; также на этом этапе не могут встретиться команды из одной группы и страны. На последующих стадиях никаких ограничений на потенциального соперника не накладывается.

Будем рассматривать жеребьевки последних 5 сезонов и добавим 1/8 финала этого года. Жеребьевка четверть- и полуфиналов до 2012 года проходила одновременно, поэтому исключим полуфинал сезона 11/12. Итого, имеем выборку из 15 жеребьевок.

Сила команды

Введем ФС, адекватно отображающую относительную силу команды:

ФС = 1/3 * РК + 2/3 * ОМ * РС, где:

РК - рейтинг клуба в таблице коэффициентов УЕФА на момент жеребьевки (считается за 5 последних лет). Переменная отражает в первую очередь так называемый “еврокубковый опыт”. Берется с весом 1/3.

ОМ - среднее количество очков за матч, набираемых командой в чемпионате своей страны.

РС - рейтинг страны в таблице коэффициентов УЕФА на момент жеребьевки (так же считается за 5 последних лет). Таким образом, произведение ОМ * РС показывает силу команды во внутреннем первенстве с учетом силы чемпионата. Второе слагаемое берется с бо́льшим весом, так как уровень команды в рассматриваемом сезоне кажется более важным показателем, чем опыт еврокубков. Считать силу команды по выступлению в группе ЛЧ текущего сезона было бы неправильно, так как, во-первых, все команды, дошедшие до определенной стадии, имеют схожее количество побед/очков, во-вторых, малое число игр в рамках Лиги Чемпионов будет вызывать большие погрешности.

Все переменные нормированы так, что среднее по каждой жеребьевке для каждой переменной равно единице.

Понятно, что идеальной эту функцию назвать нельзя, но такой вид кажется оптимальным с учетом простоты подсчета. Проверка на адекватность значений не дала никаких неожиданных результатов.

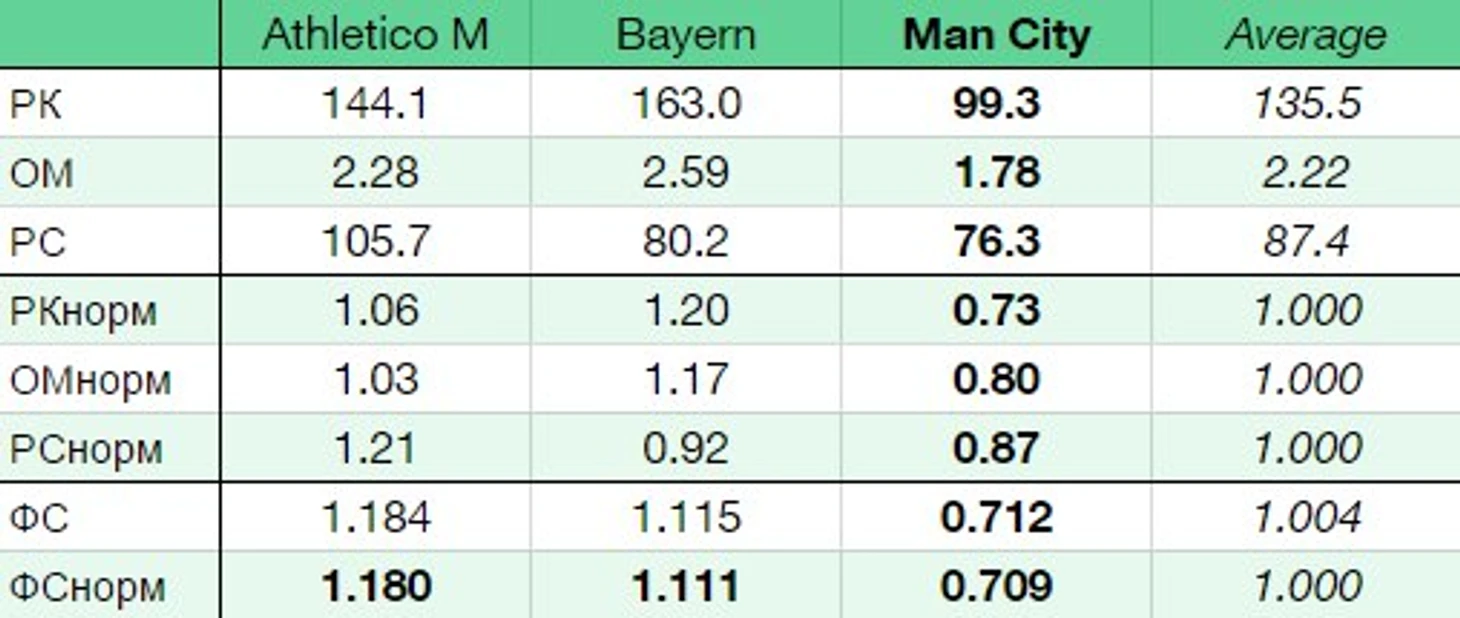
Пример расчета ФС для жеребьевки полуфинала предыдущего сезона

Рейтинг силы

Как уже было отмечено, отсортируем значения ФС по возрастанию. Пусть команда заняла i-ое место по этому показателю среди n команд. Тогда найдем РС следующим образом:

РС = i/(n+1)

Среднее значение для одной жеребьевки равно 0,5. Стандартное отклонение рассчитанного по такой формуле рейтинга примерно одинаково (от 0,25 до 0,27) для любых возможных n. Из этого следует, что более высокая вероятность выпадения слабейшей команды на стадии полуфинала (3 потенциальных соперника), чем на стадии 1/4 или 1/8 (5-7 соперников), адекватно учитывается при расчете РС.

Взглянем на получившуюся картину:

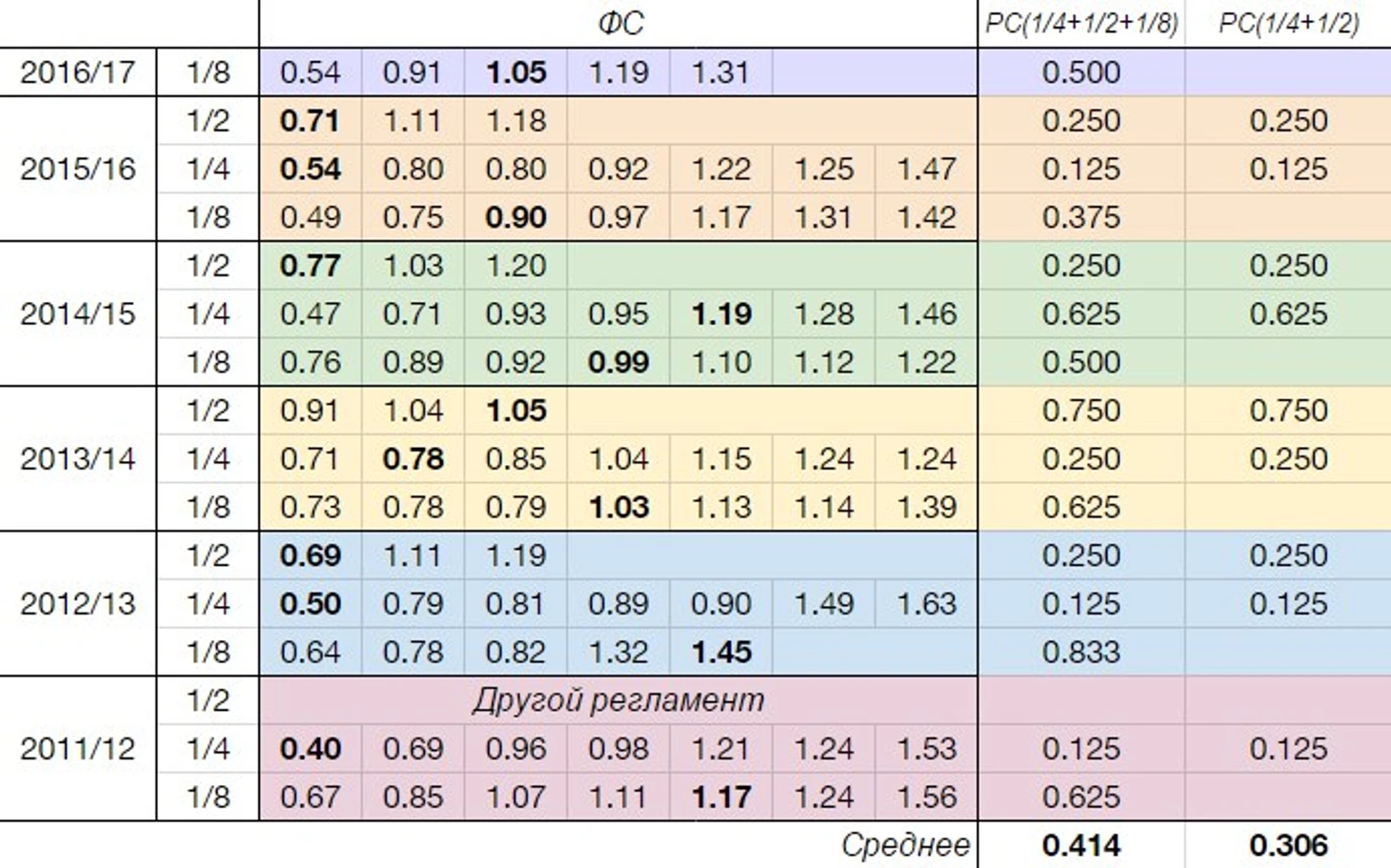
Жирным выделены выпавшие мадридскому Реалу команды. Как видно, шесть раз это были слабейшие команды и только дважды - сильнейшие; впрочем, сами по себе эти факты ни о чем не говорят.

Заметим, что соперников, выпадавших на стадии 1/8 ни в одном из случаев нельзя назвать относительно слабыми. Помимо выборочного среднего по всей выборке найдем и выборочное среднее только для полу- и четвертьфиналов - это значение указано в последнем столбце таблицы.

Полная выборка

Рассмотрим, насколько маловероятно получившееся выборочное среднее для всех рассматриваемых жеребьевок. Согласно центральной предельной теореме, распределение выборочных средних, при условии достаточно большого n, будет стремиться к нормальному. Обратим внимание, что проверяемое нами распределение является дискретным, что, тем не менее, не будет являться проблемой при его приближении непрерывным. Оценим сверху дисперсию нормального распределения, приближающего распределение выборочных средних по выборке объема n = 15. Матожидание, очевидно, будет равняться 0,5.

Проведя 200 000 симуляций по 15 жеребьевок в каждой, мы получили распределение выборочных средних, которое хорошо приближается нормальным с ожиданием 0,5 и стандартным отклонением 0,068. Вычисление площади под графиком слева от значения 0,414 дает квантиль 10%. Заметим, что эта величина является оценкой сверху, следовательно, минимум в 90% случаях жребий был бы менее благосклонен к команде из Мадрида.

Полу- и четвертьфиналы

Разумно заметить, что уровень Реала позволяет проходить стадию 1/8 финала без малейшей оглядки на соперника. А вдруг воздействие на результаты жеребьевок происходит только на следующих стадиях?

Проведем те же самые операции для выборочных средних по выборке объема n = 9. Получим следующую картину:

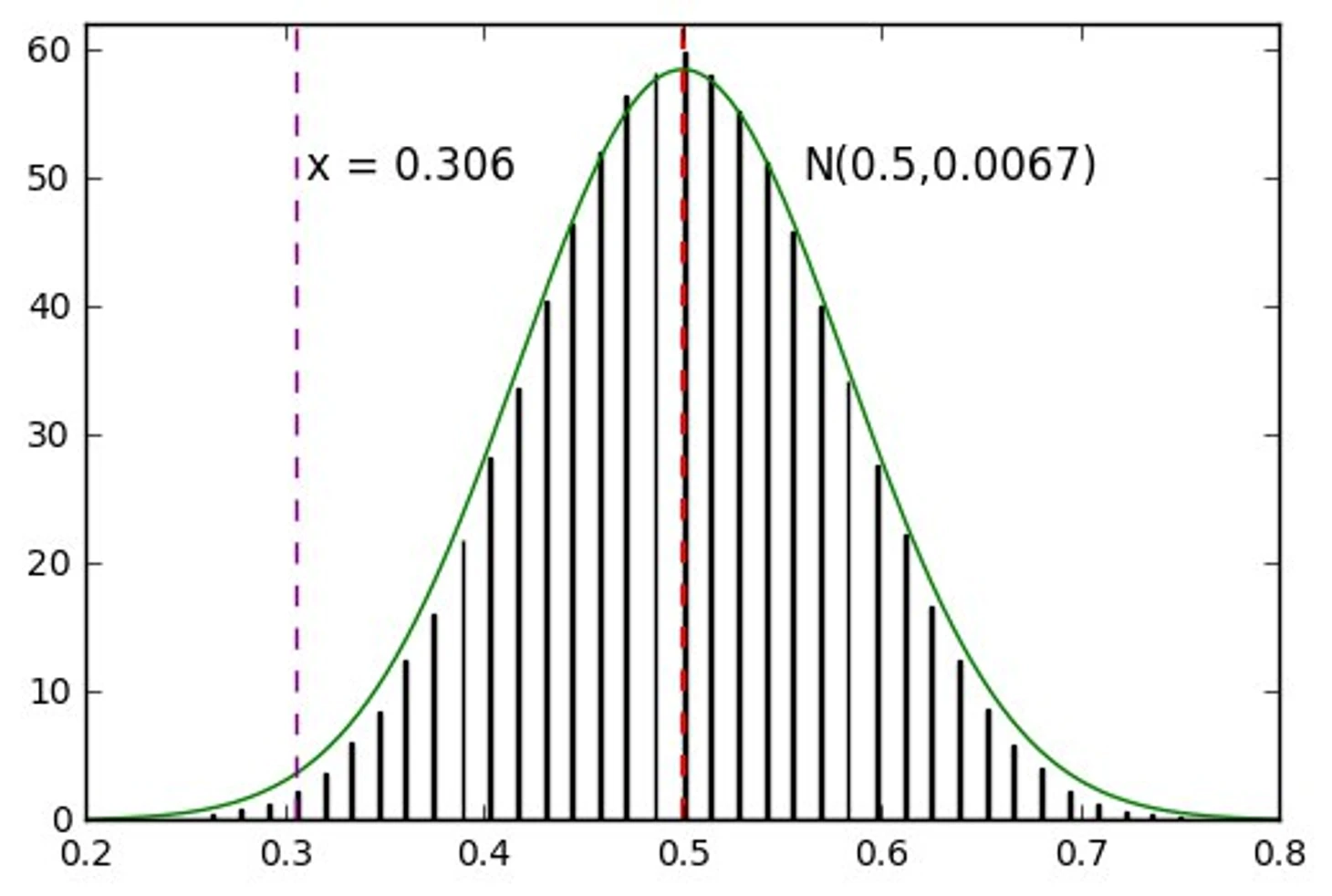
Проведя те же 200 000 симуляций 9 жеребьевок, получаем, что наше дискретное распределение очень хорошо приближается сверху нормальным со стандартным отклонением 0,082. Значение 0,306 оказывается на границе 1%-го квантиля. Это означает, что как минимум в 99% случаев жребий был бы менее благосклонен к мадридскому Реалу.

Толкование результатов

Полученные цифры показывают, что на стадии 1/8 финала махинации при жеребьевке со стороны Реала крайне маловероятны, так как выпадавшие соперники в среднем не слабее потенциальных. Однако, на последующих стадиях средний соперник входит в 1% самых слабых из возможных, что вызывает сильные подозрения. Впрочем, это не может считаться прямым доказательством вины Переса, ведь помня о серии Акинфеева, в нашем мире случаются и более редкие серии событий.

Любите математику и помните о трех видах лжи.

Еще больше аналитики вы найдете в паблике Блокнот.

logoФлорентино Перес
logoЛига чемпионов УЕФА
logoРеал Мадрид