Сколько надо xG, чтобы забить гол
Все вы, конечно, много читали об xG, о достоинствах и недостатках этой системы, и думали, насколько точно она отражает действительность, а не какие-то абстракции. Я уже замечал месяц назад, что в идеале показатель xG должен равняться вероятности забить гол в данной ситуации. Однако так ли это? После последнего тура РФПЛ и града голов ваша вера в этот факт серьёзно пошатнулась, однако у меня ещё есть доводы в его пользу.
Дальше я буду оценивать то, насколько xG близок к вероятности забить гол, с помощью некоторых статистических метрик. Если вдруг вам не интересна громоздкая математика, а любопытен только ответ, то вот он: 0,92 - именно столько в среднем надо xG, чтобы забить один гол. При этом если удары с xG между 0,2 и 0,4 искусственно сделать чуть дороже (достаточно пары сотых), то мы получим идеальное равенство, что в среднем 1 xG равен 1 голу.
Теперь чуть более детально. Все вычисления проводились на накопившейся у нас базе матчей текущего сезона, которая содержит в сумме 20943 удара (без учёта пенальти). Это не очень много, но уже достаточно, чтобы приводить какие-то оценки. Первое, на что мы обратим внимание, это то, как часто встречаются удары с разными xG. Поскольку голы - события редкие, то логично, если модель xG будет довольно консервативна в своей оценке и будет давать большие вероятности только редким по-настоящему опасным ударам.

На графике шкала у логарифмическая, т.е. значит, что цена ударов в модели xG распределена экспоненциально, т.е. удары за 0.01 xG встречаются в 10 раз чаще, чем удары за 0.25 и в 100 раз чаще, чем удары за 0.5. Это вполне отвечает нашим ожиданиям от модели.
Далее посмотрим на то, как сильно в среднем ошибается модель в своём предсказании. Если мы просуммируем все xG всех имеющихся ударов и поделим их на количество голов, то мы получим оценку сколько в среднем приходится xG на 1 гол. В выборке ударов было 1992 гола, а все удары в сумме дали 1842.2 xG, простое деление даёт нам число 0.925 xG на 1 гол. Однако насколько сильно можно доверять такой оценке? Вдруг нам просто повезло? Для того, чтобы ответить на этот вопрос, вычислим доверительный интервал для этой величины: промежуток, в котором она лежит с вероятностью 95%. Напрямую это сделать не получится, поэтому оценим вначале другую величину.
Для каждого удара вычтем из xG 1, если удар закончился голом, и 0, если нет. Полученная величина отражает ошибку оценки каждого удара. Посмотрим на распределение этой ошибки:
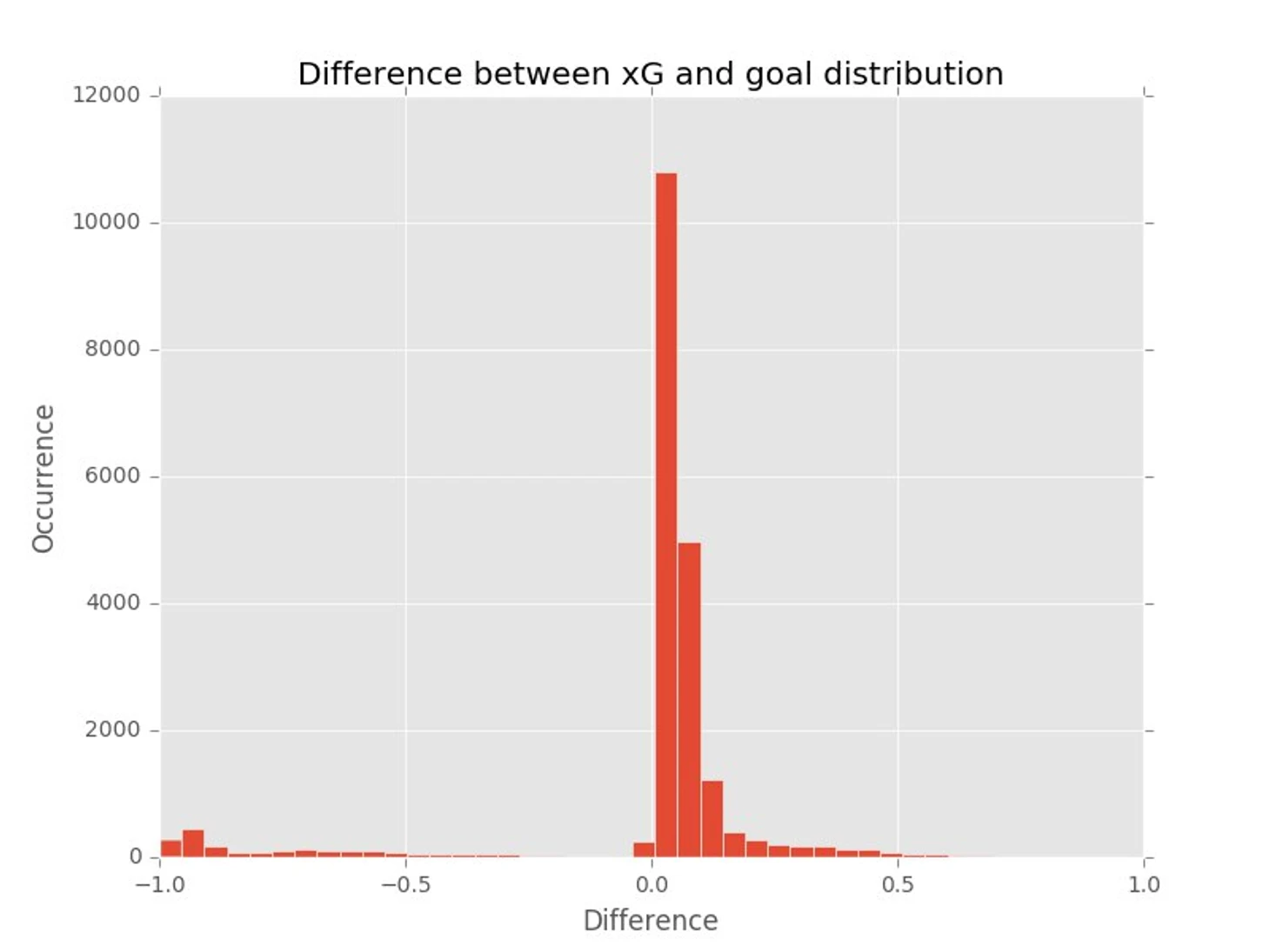
Чаще всего, как мы знаем из распределения xG, мы будем встречать удары с маленьким показателем, которые будут довольно редко оказываться голами, отсюда куча положительных ошибок чуть больше нуля. Однако часть этих ударов таки окончится голами и они будут давать результаты в окрестности -1. Распределение это не совсем нормальное (всё из-за дополнительного бугорка в районе -0,95), однако центральная предельная теорема всё равно позволяет нам оценить доверительный интервал для среднего значения этой ошибки. Само среднее равно -0.007, т.е. каждый удар недооценивает в среднем вероятность гола на 7 тысячных. Это не очень много, но на масштабе 20000 ударов превращается в сотню потерянных голов. Посмотрим же на то, как меняется эта величина и её доверительный интервал во времени (а точнее их зависимости от количества ударов):
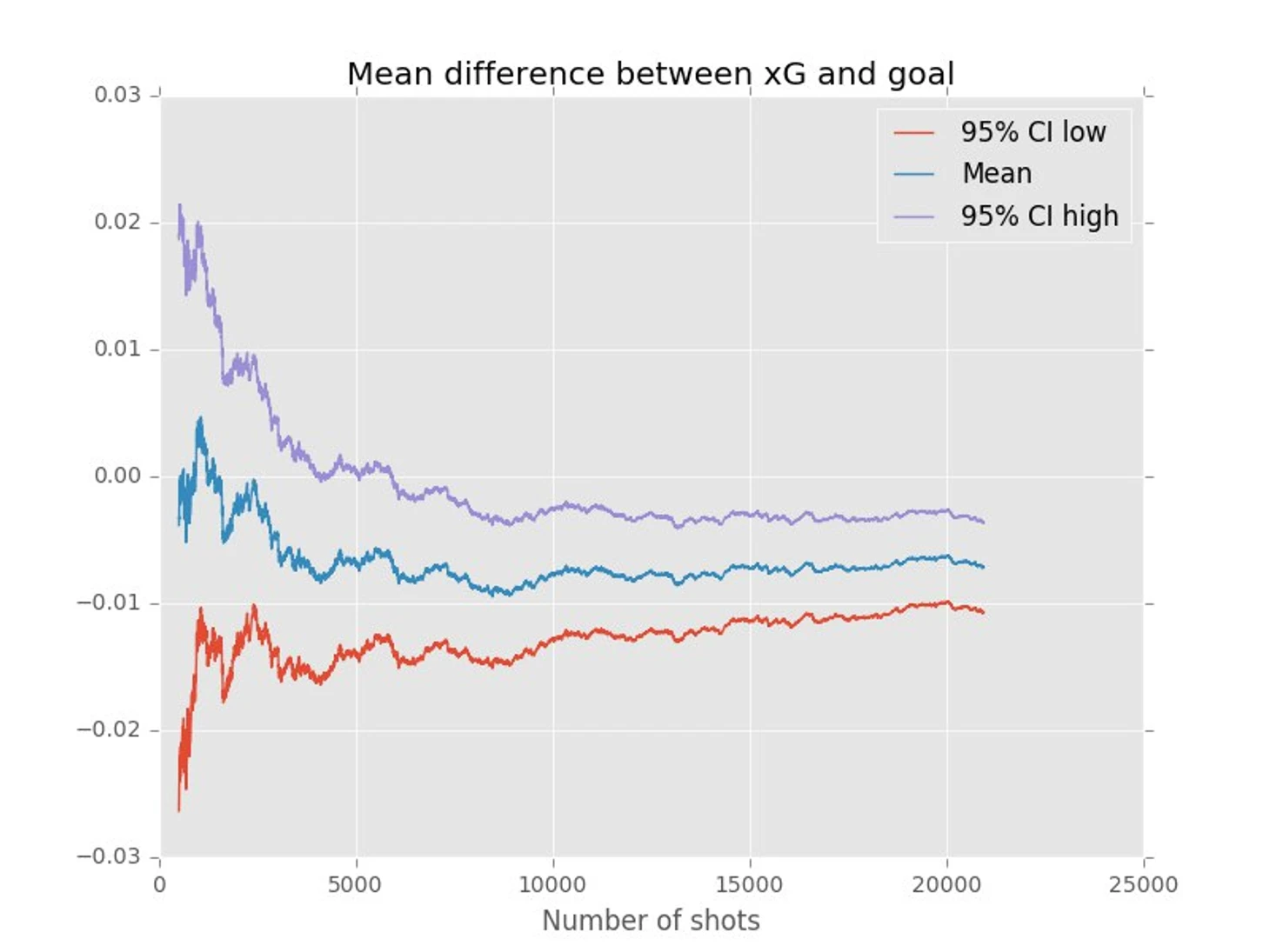
Мы получили, что с вероятностью 95% средняя ошибка на удар лежит в интервале между -0.011 и -0.0036. Как видно из графика, со временем эта величина перестала сильно меняться и относительно стабилизировалась, что есть хорошо. Теперь, когда мы знаем оценку на ошибку от одного удара, посмотрим, сколько голов мы должны были потерять на всех 20943 ударах, для этого просто прибавим к сумме голов эту величину, умноженную на количество ударов, и поделим на число голов. Таким образом мы получим доверительный интервал, в котором с вероятностью 95% лежит отношение суммы xG к сумме голов.
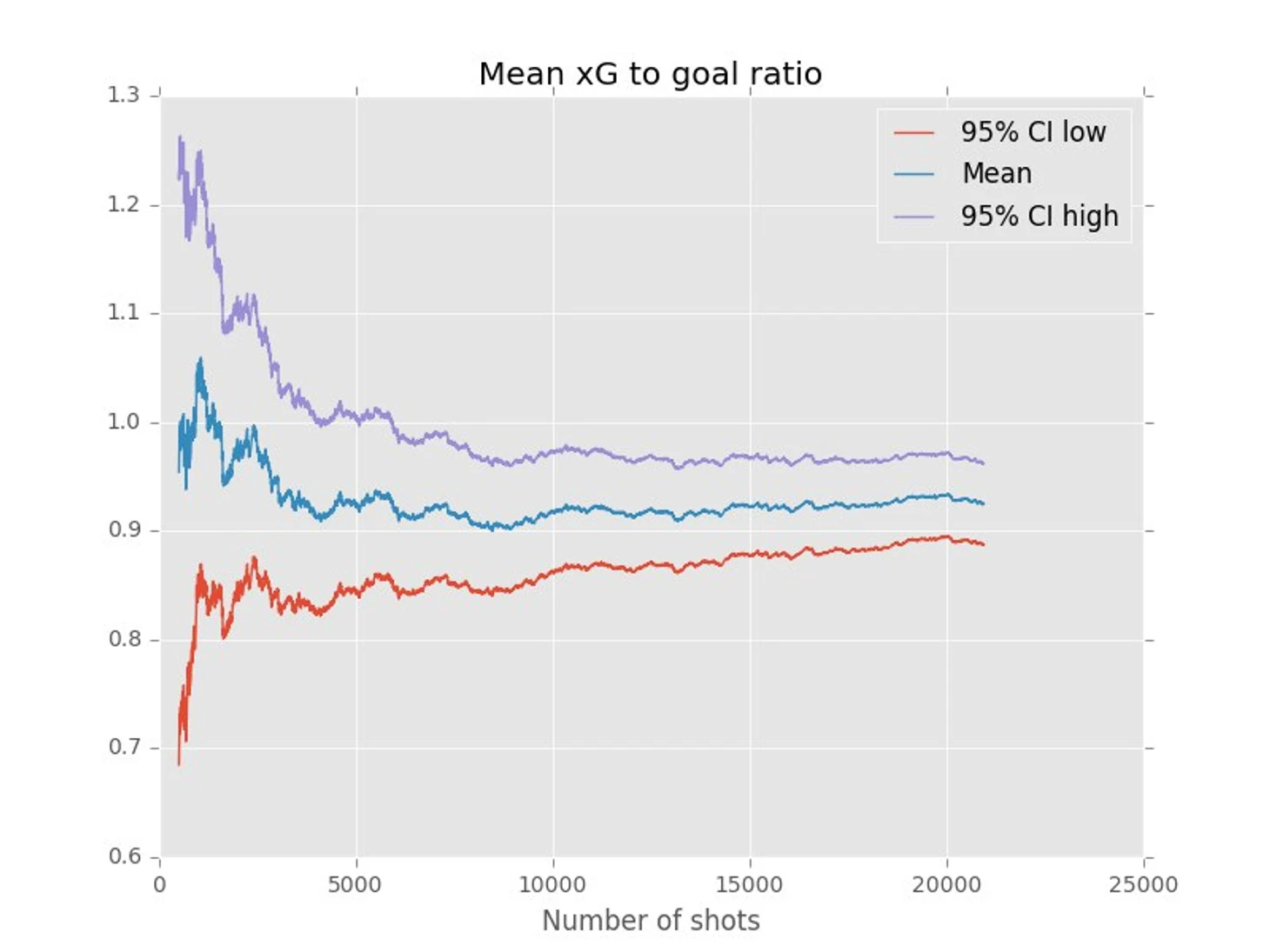
Получаем, что с вероятностью 95% 1 голу соответсвует xG в интервале между 0.888 и 0.962. Отличные числа! Плохие новости, что шансов на то, что отношение достигнет ровно 1, как нам хотелось бы, мало, но зато далеко от 0.92 оно тоже уже не убежит, а это хоть и ошибка, но не такая существенная, как если бы мы получили отношение 0.5, например. Поэтому методику ожидаемых очков мы перелопачивать пока не будем и будем продолжать обращаться с xG, как с вероятностью забить. Тем более, у меня есть ещё одна метрика в запасе!
До этого мы меряли среднюю температуру по больнице, хорошо, что она нормальная, но было бы неплохо, если бы всё было отлично и в каждом отделении. Для этого возьмём удары с xG, лежащими в заданном интервале, например, между 0.6 и 0.7, всего таких ударов набралось 149. Если xG это вероятность забить, то нам хотелось бы, чтобы среди этих ударов было примерно 65% голов. Голов там 95, т.е. примерно 64%, что не очень далеко от истины. Если теперь мы отложим для каждого небольшого интервала точку (среднее xG ударов в интервале, процент голов), то получим так называемую калибровочную кривую:

Интервалы после 0,65 я не оценивал, потому что ударов в них мало и оценка неточна. Зато для всех остальных интервалов среднее xG очень близко к пропорции голов, и значит можно утверждать, что xG примерно равен вероятности гола! Самое большое расхождение можно увидеть для ударов с xG между 0,2 и 0,4, однако даже для них несоответствие составляет пару сотых. Для интервалов же меньше 0,2, где сконцентрировано подавляющее большинство ударов (а значит оценка там наиболее точна), мы получаем идеальное совпадение вероятности гола и xG!
На этом мои доводы заканчиваются. Вывод из всей этой истории один: xG - сила! И этот показатель очень хорошо подобран, чтобы оценивать вероятность гола в различных ситуациях.











Наверное имелось в виду отношение xG на гол. И исследование разных чемпов давало бы пищу для размышлений.