Трибуна
9 мин.

Баскетбол – это случайное блуждание. Это доказывает математическая модель

3

Перед вами выжимка статьи Random Walk Picture of Basketball Scoring by A. Gabel and S. Redner. В ней авторы посмотрели на баскетбол с физико-математических позиций. Взялся за статью больше для себя, поэтому даже выжимка будет с одной стороны непростой для чтения, а с другой – далекой от академической точности. Если не идет или сильно раздражают неточности – смело закрывайте вкладку.

Введение

Благодаря большому количеству забитых мячей баскетбол хорошо подходит для статистического анализа. Цель статьи – исследовать статистически разницу в счете в течение одной игры и ответить на вопрос, является ли эта метрика результатом стохастического процесса без памяти (А) или же результатом нескольких процессов с долговременной корреляцией (Б).

Похожий вопрос – существует ли эффект горячей руки – был тщательно изучен ранее и объясняется скорее вариантом А.

С точки зрения обычного болельщика длительные голевые серии и засухи видятся экстраординарными событиями и соответственно требуют особых объяснений и особых действий от тренеров и игроков – это вариант Б. 

Авторы проанализировали основное время 6087 игр НБА с 2006/07 по 2009/10. В результате исследования построили такую модель:

  1. Основа – случайное блуждание с непрерывным временем

  2. Это блуждание антиперсистентное

  3. При этом действует слабая восстанавливающая сила

Эта модель хорошо согласуется с данными игр, т.е. можно сказать, что в реальности действует что-то близкое к варианту А. 

Скорость набора очков

Эпизод набора очков – все очки, набранные командой без паузы в игровом времени, т.е либо просто попадание с игры, либо штрафные, либо попадание + штрафные. Доля эпизодов с одним очком равна 8.7%, с двумя – 73.9%, с тремя – 17.3%, с четырьмя и выше – меньше 0.2%. В среднем 1 эпизод приносит 2.09 очка. 

Скорость набора очков – количество эпизодов в секунду. Для выборки скорость получилась 0.03291 эпизода/сек. Она почти не меняется от сезона к сезону, и довольно стабильна в течение игры за исключением падения в самом начале каждой четверти (никто не бросает на первой секунде) и скачка в конце каждой четверти (все оттягивают свой бросок до последних секунд):

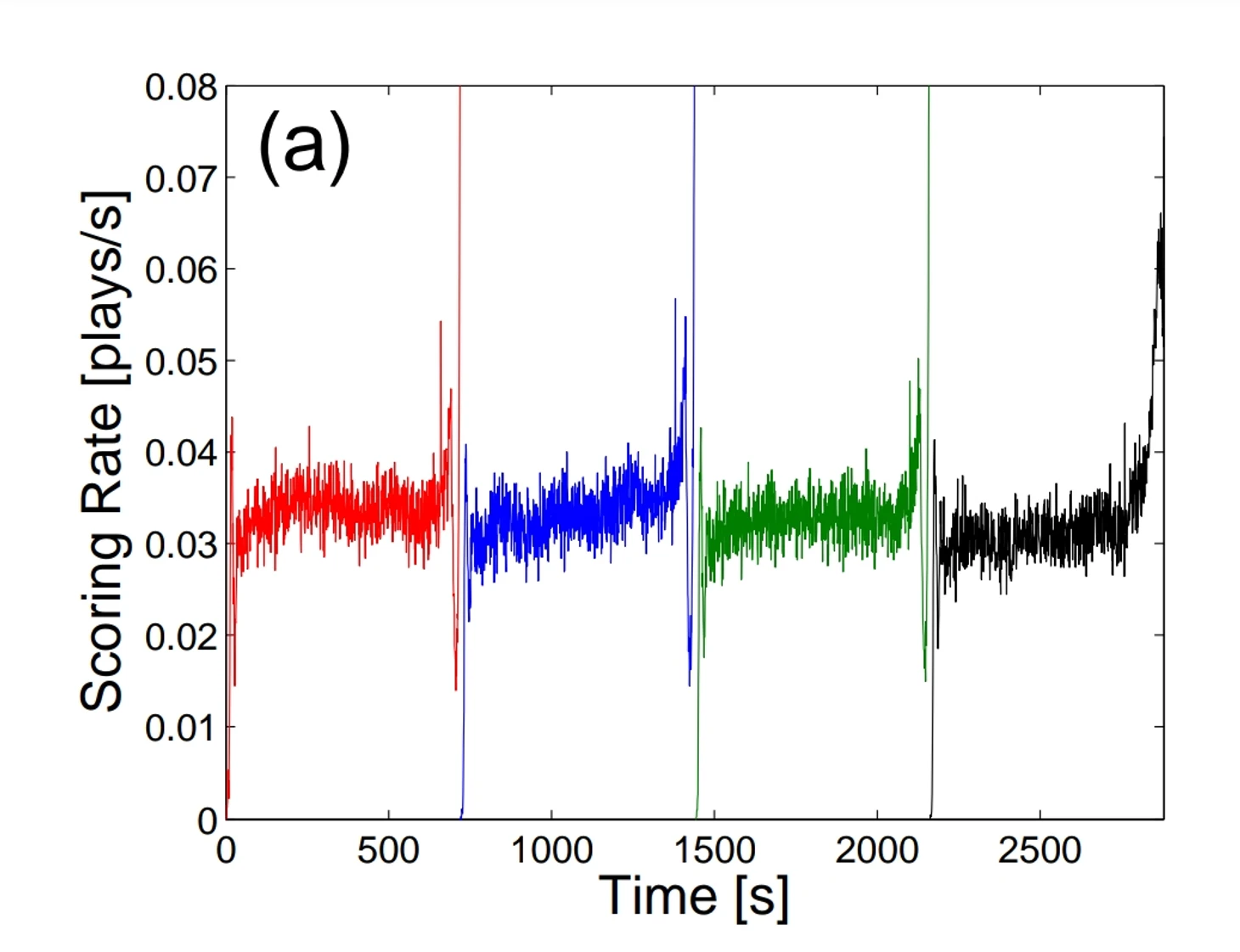
По оси Х – время, вертикальные линии – границы четвертей. По оси У – скорость набора очков.

Еще больший скачок в конце 4ой четверти – результат ускорения игры проигрывающей командой и тактических фолов.

Время до следующего забитого

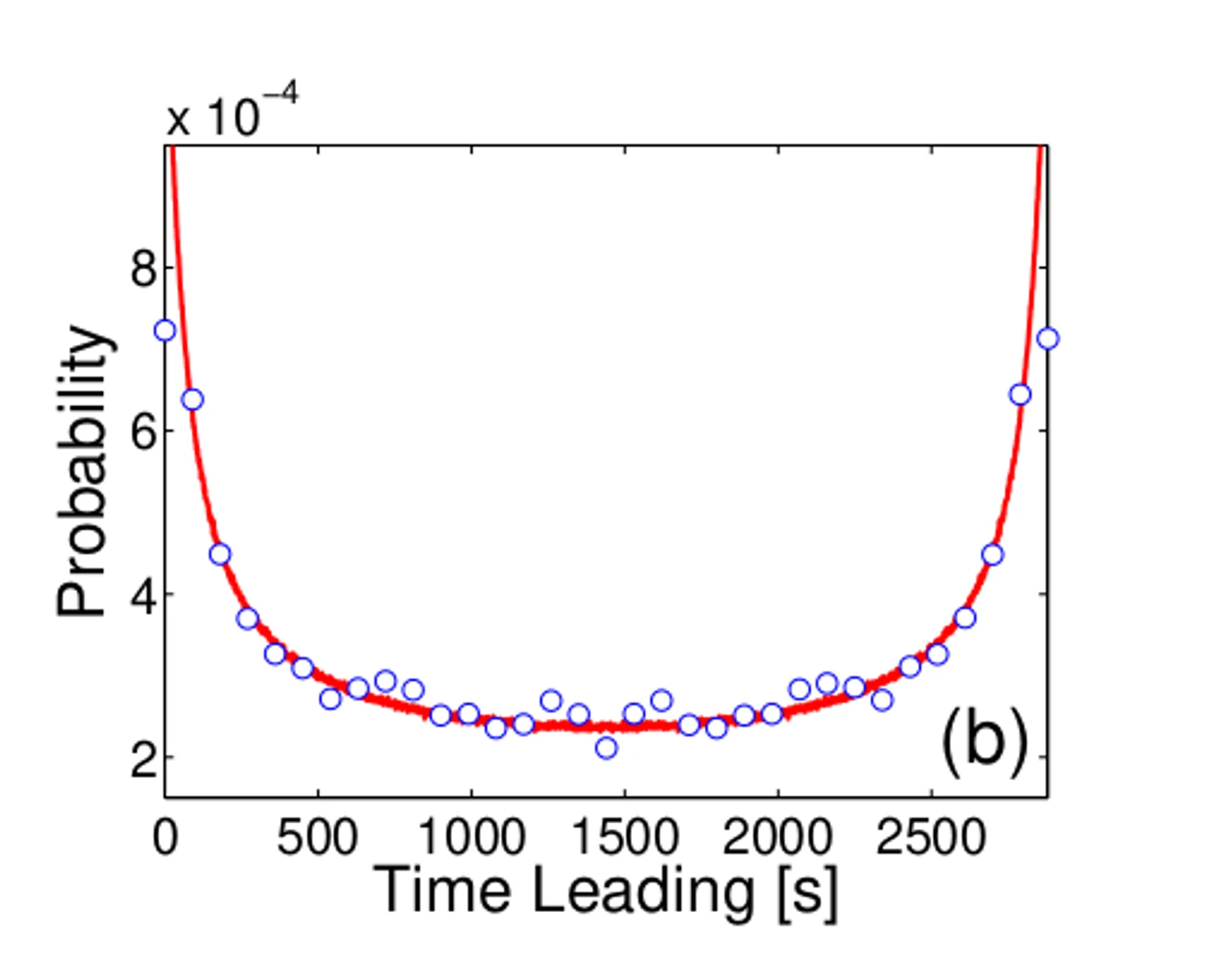
t_e – сколько времени прошло до следующего эпизода набора очков любой из команд, t_s – сколько времени прошло до следующего эпизода набора очков той же самой команды. Пик вероятности для t_e приходится на 16 секунд. Потому что после пропущенного мяча у команды есть 24 секунды на то, чтобы забить самой. Распределение t_s повторяет растянутое по времени в 2 раза распределение для t_e, с пиком на 32ой секунде.

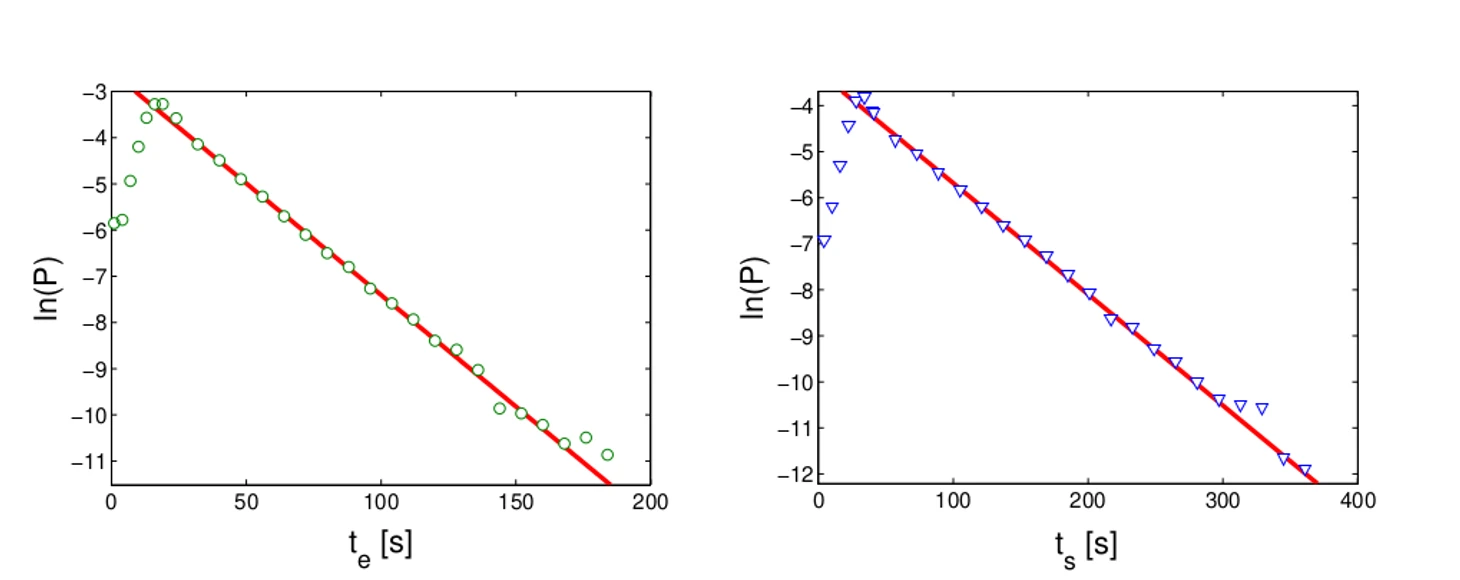
По оси Х – времена t_e и t_s в секундах, по оси У – логарифм вероятности, что прошло именно столько времени.

По большей части зависимость экспоненциальная. Графики линейные из-за логарифмирования оси У. 

Авторы проверили корреляции между временем соседних эпизодов набора очков и выяснили, что она очень мала. Следовательно, мы имеем дело с процессом (почти) без памяти. Значит, все серии попаданий и голевые засухи могут быть объяснены характеристиками этого процесса. 

Процесс без памяти: на время до каждого следующего эпизода не влияет ни история предыдущих эпизодов, ни уже прошедшее ожидание. Пример: если рыба клюет случайно, но с некоторой фиксированной средней интенсивностью, то количество времени, уже затраченное рыбаком на ожидание следующей поклевки, не влияет на время, которое ему ЕЩе придется прождать.

Общий счет за игру

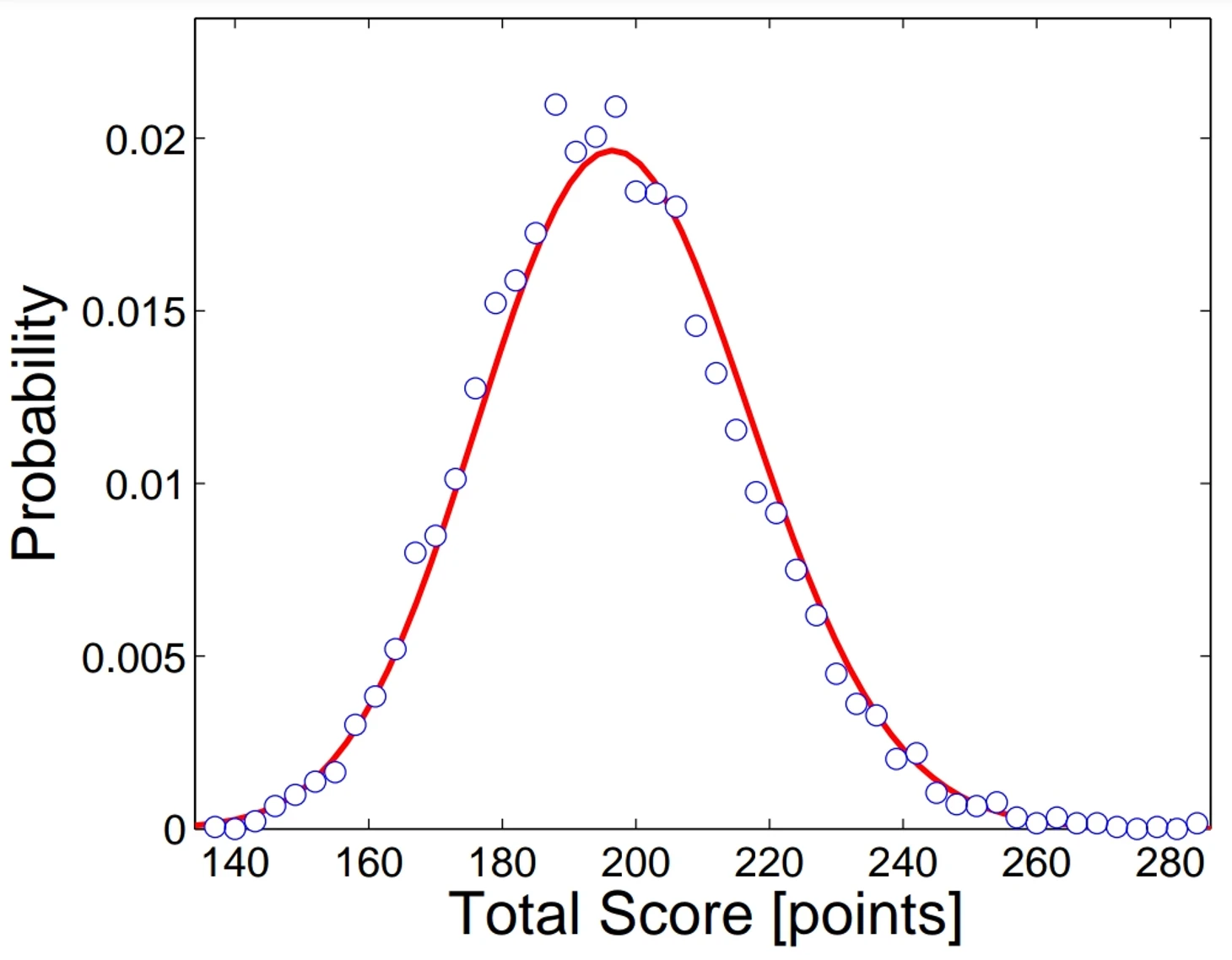
Один эпизод набора очков приносит 2.09 очка и случается в среднем каждые 30.4 секунды. Предположили, что набор очков – это обычный пуассоновский процесс.

Пуассоновский процесс: есть поток некоторых случайных событий, идущих одно за другим, и количество событий за отрезок времени следует распределению Пуассона. 

Тогда можно рассчитать теоретическое распределение суммы очков обеих команд на исходе 4ой четверти по формуле и сравнить с тем, что было в реальных играх:

По оси Х – количество очков. По оси У – вероятность, что команды суммарно к концу 4ой четверти набрали именно столько очков. Красная линия – вычисление по формуле, синие окружности – статистика на основе реальных игр.

Длина серии попаданий подряд одной команды

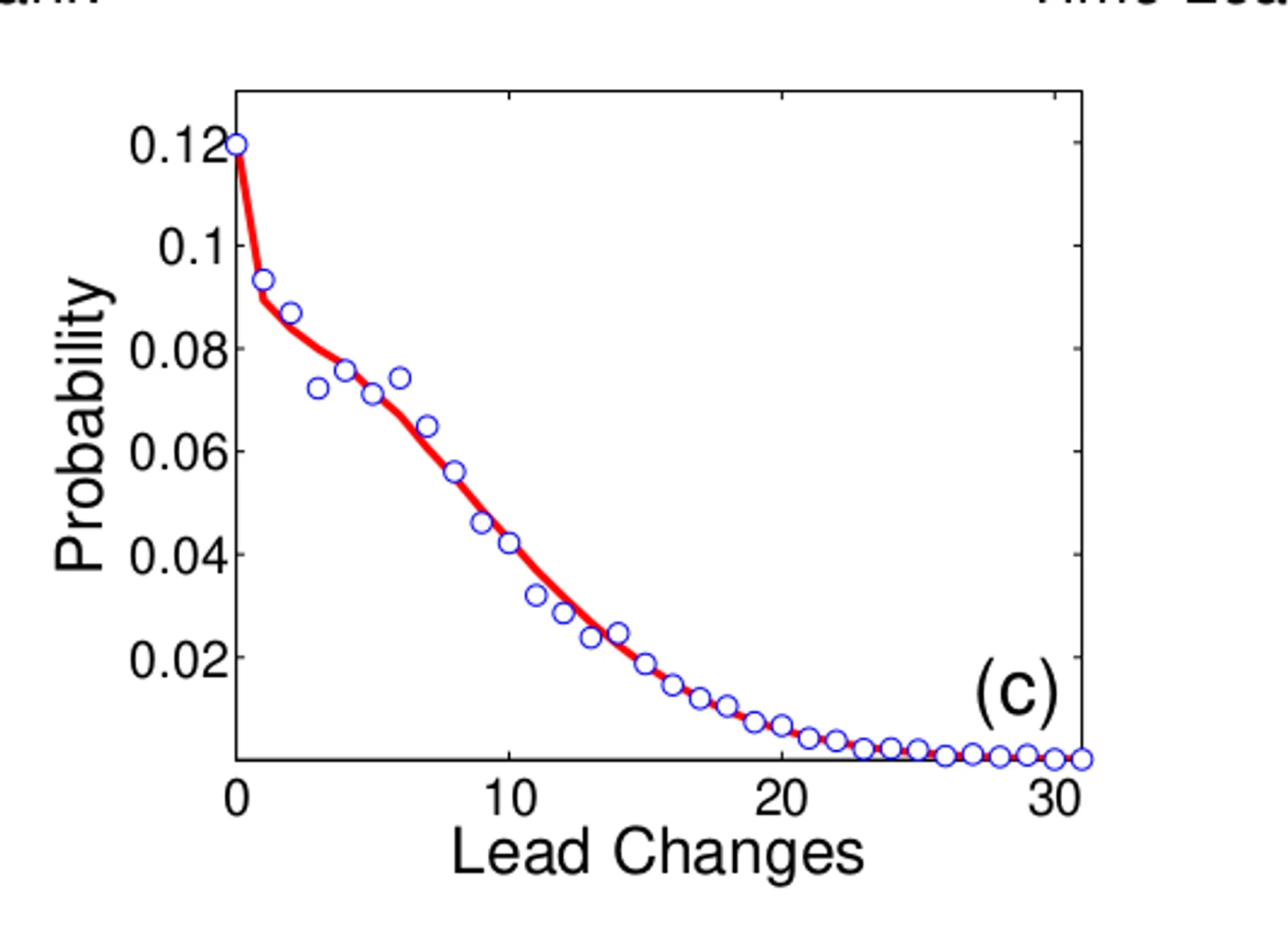
Антиперсистентность – сразу после забитого мяча вероятность, что следующей забъет та же самая команда, равна 34.8%, а вероятность, что это сделает только что пропустивший соперник, –  65.2%. Это прямой результат перехода владения после забитого мяча. Из этого и среднего количества очков для одного эпизода набора (примерно 2.09) можно составить модель экспоненциального затухания для вероятности количества очков, которые одна команда набирает подряд. 

Экспоненциальное затухание: вероятность забить еще после уже забитого – 34.8%, вероятность забить еще 2 раза подряд – 34.8% * 34.8% = 12.1%, еще 3 раза – 34.8% * 34.8% * 34.8% = 4.2% и так далее. 

Если учесть, что за эпизод набора очков команда может заработать 1, 2, 3 или 4 очка с разной вероятностью, то получится чуть более сложная модель, которая лучше соотносится с тем, как часто серии разной длины происходили на самом деле:

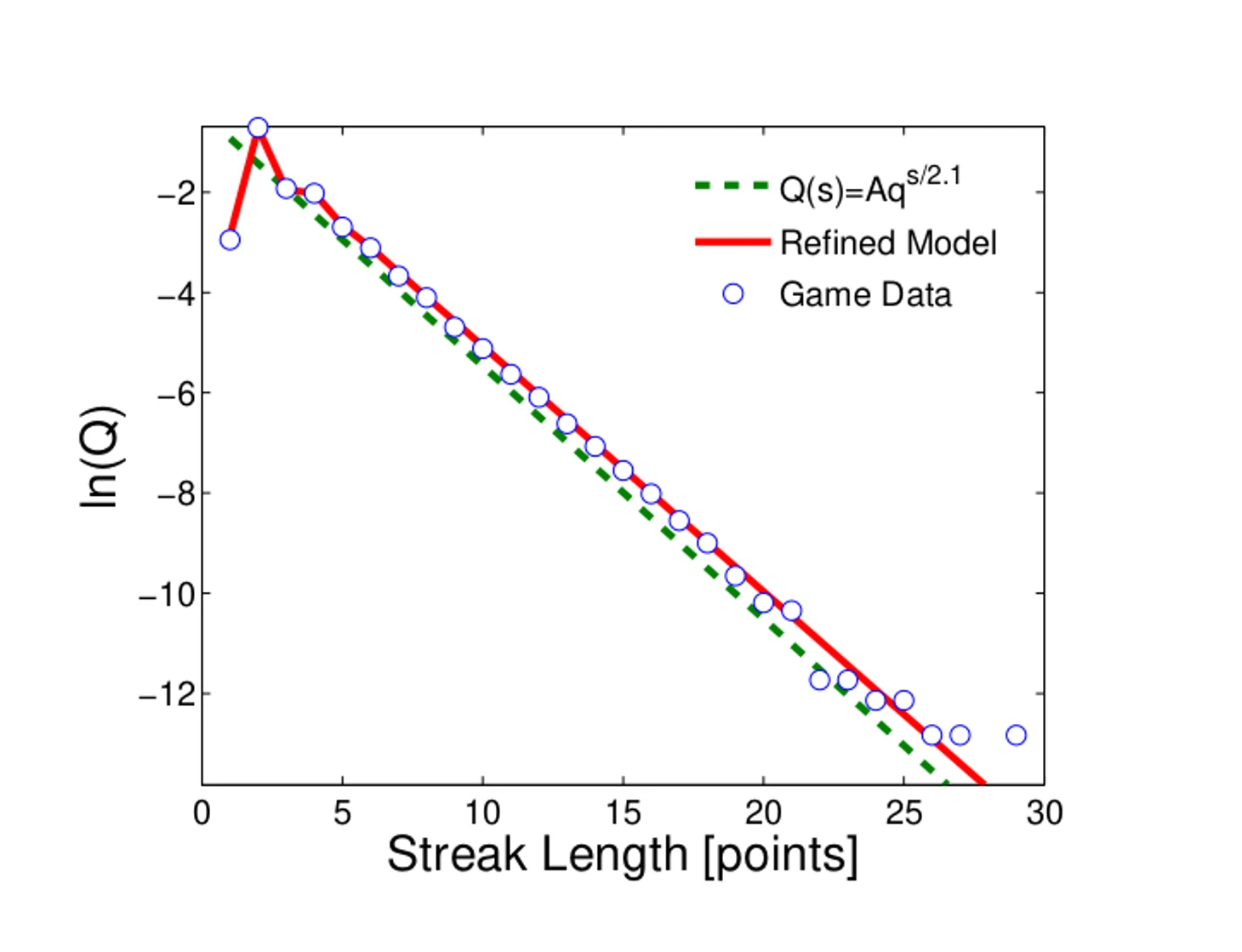
По оси Х – количество очков. По оси У – логарифм вероятности, что одна команда наберет подряд именно столько очков. Зеленая линия – вычисление по простой формуле, красная линия – более сложная модель, синие окружности – статистика на основе реальных игр.

Вероятность забить зависит от разницы в счете

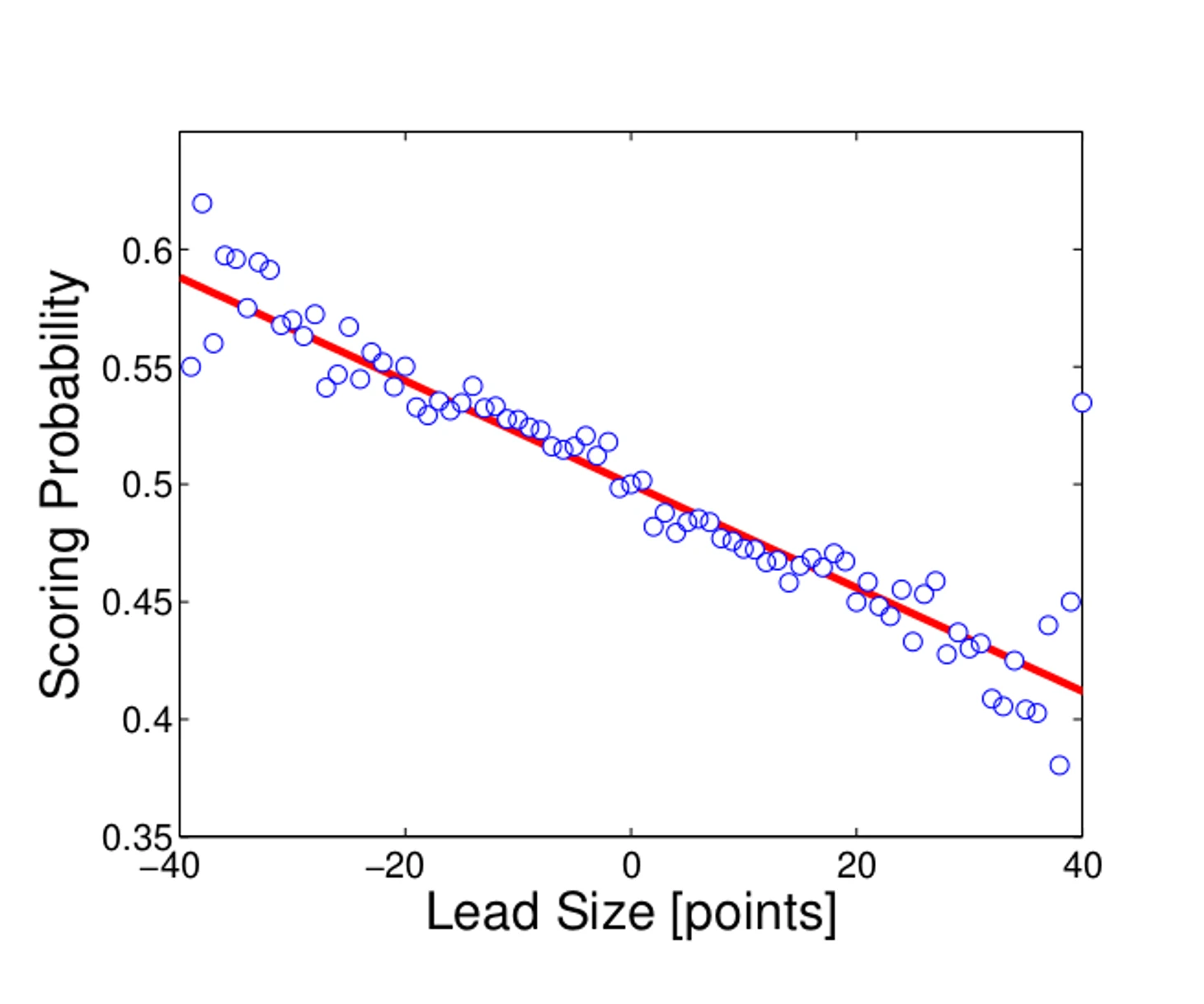
По оси Х – количество очков. По оси У – вероятность ведущей в счете команды набрать очки, если ее отрыв от соперника составляет именно столько очков. Красная линия – простая линейная регрессия, синие окружности – статистика на основе реальных игр.

Наивное объяснение: команда, которая далеко впереди по счету, начинает экономить силы и в защите и в нападении, а ее соперник, наоборот, старается изо всех сил.

Важно, что этот эффект:

  • очень близок к линейному – так его проще учитывать

  • довольно мал по своему влиянию – скорость набора очков падает всего лишь на 0.0022 на каждое очко положительной разницы в счете 

Авторы назвали это линейной восстанавливающей силой.

Случайное блуждание

Опишем разницу в счете в момент времени t. В момент стартового спорного разница очевидно равна нулю. И она меняется в ту или другую сторону в зависимости от того, сколько очков и какая команда их набрала в каждом следующем эпизоде. Как мы убедились ранее это случайный процесс. Тогда разницу в счете можно представить как  одномерное случайное блуждание. Для такого блуждания характерна линейная зависимость разброса от времени, что подтверждается данными для всей длины игру кроме последних 2-3 минут:

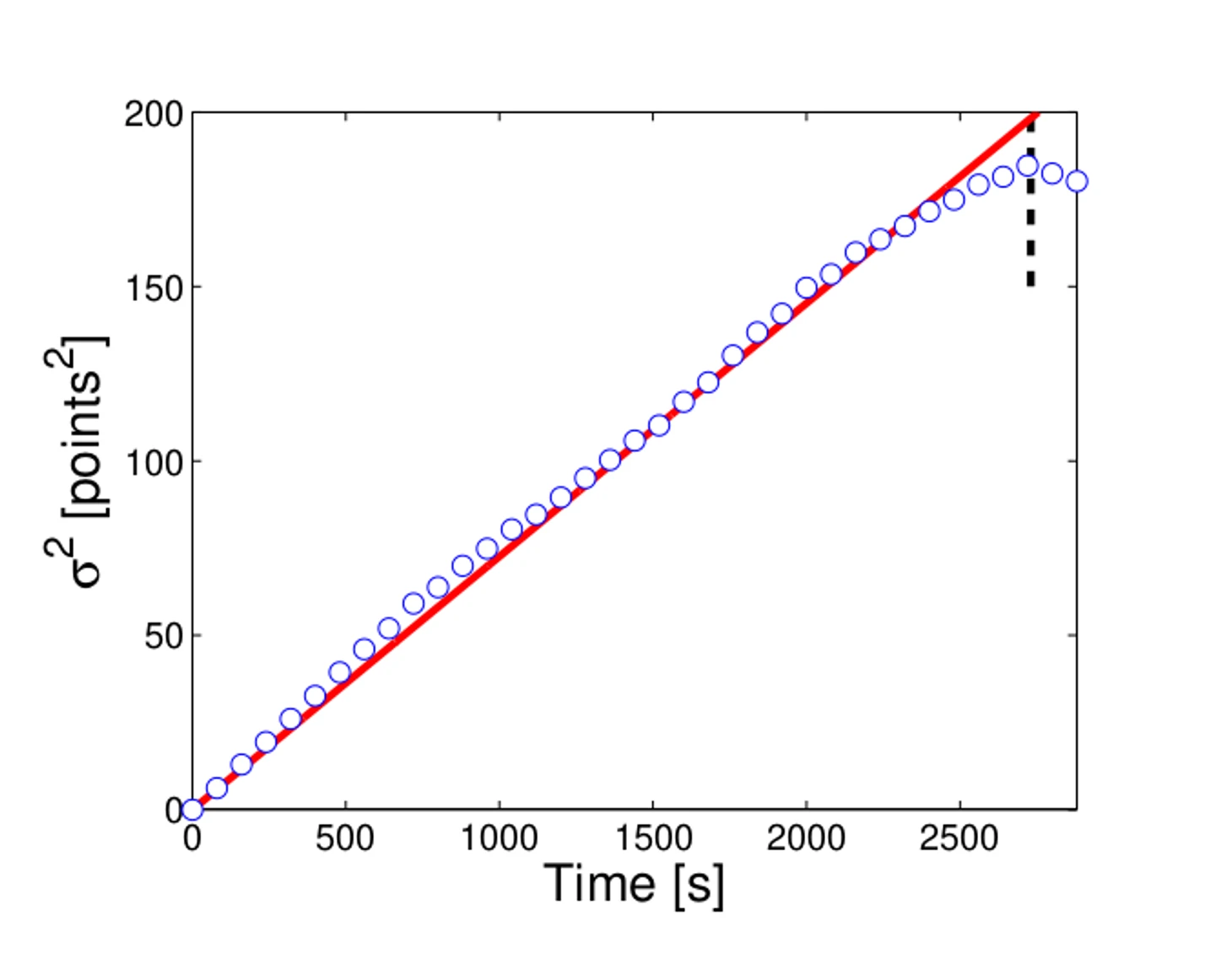
По оси Х – количество секунд от начала матча. По оси У – дисперсия разницы в счете в этот момент игрового времени. Красная линия – простая линейная регрессия, синие окружности – статистика на основе реальных игр, черный пунктир – последние 2.5 минуты основного времени.

В первом подходе авторы считали обе команды равными по силе, т.е. разница может пойти вверх или вниз с равной вероятностью. В реальности же есть сильные команды и есть слабые. Чтобы это учесть, команды разделили по проценту побед в конце сезона и для каждой зафиксировали ее внутреннюю силу, т.е. слабо зависящую от внешних обстоятельств и случайностей. 

Авторы показали, что влияние силы команды есть, но но не очень велико: случайность процесса оказывает на разницу в счете большее влияние и таким образом скрадывает разницу в уровне соперников. 

Вычислительная модель

Все вышеописанные штуки собрали вместе:

  • Игра – это последовательность однородных по времени и нескоррелированных между собой эпизодов набора очков

  • Время между эпизодами выбирается из распределения Пуассона 

  • Количество очков выбирается из набора 1, 2, 3, 4 в соответствии с их частотами в реальных играх 

  • Выбор того, какая команда в этот раз набрала очки, случаен, но учитывает 3 фактора: внутренняя сила команды, антиперсистентность и линейная восстанавливающая сила

  • Генерация эпизодов происходит до тех пор, пока сумма промежутков не превысит 48 минут

Так просимулировали каждую игру целого сезона. Затем сравнили результаты симуляции с реальными данными.

Результаты

По оси X – время, по оси Y – вероятность того, что команда будет за всю игру лидировать именно столько времени. Красная линия – результат симуляции, синие окружности – статистика на основе реальных игр.
По оси X – количество смен лидера, по оси Y – вероятность того, что за всю игру произойдет столько смен.
По оси Х – разница в счете в момент игрового времени t, нормированная на дисперсию разницы в счете в этот момент игрового времени.По оси У – вероятность такой нормированной разницы. Красная линия – результат симуляции для t=45.5 минут. Синие треугольники – статистика на основе первых 45.5 минут реальных игр, черные окружности – на основе 48 минут.

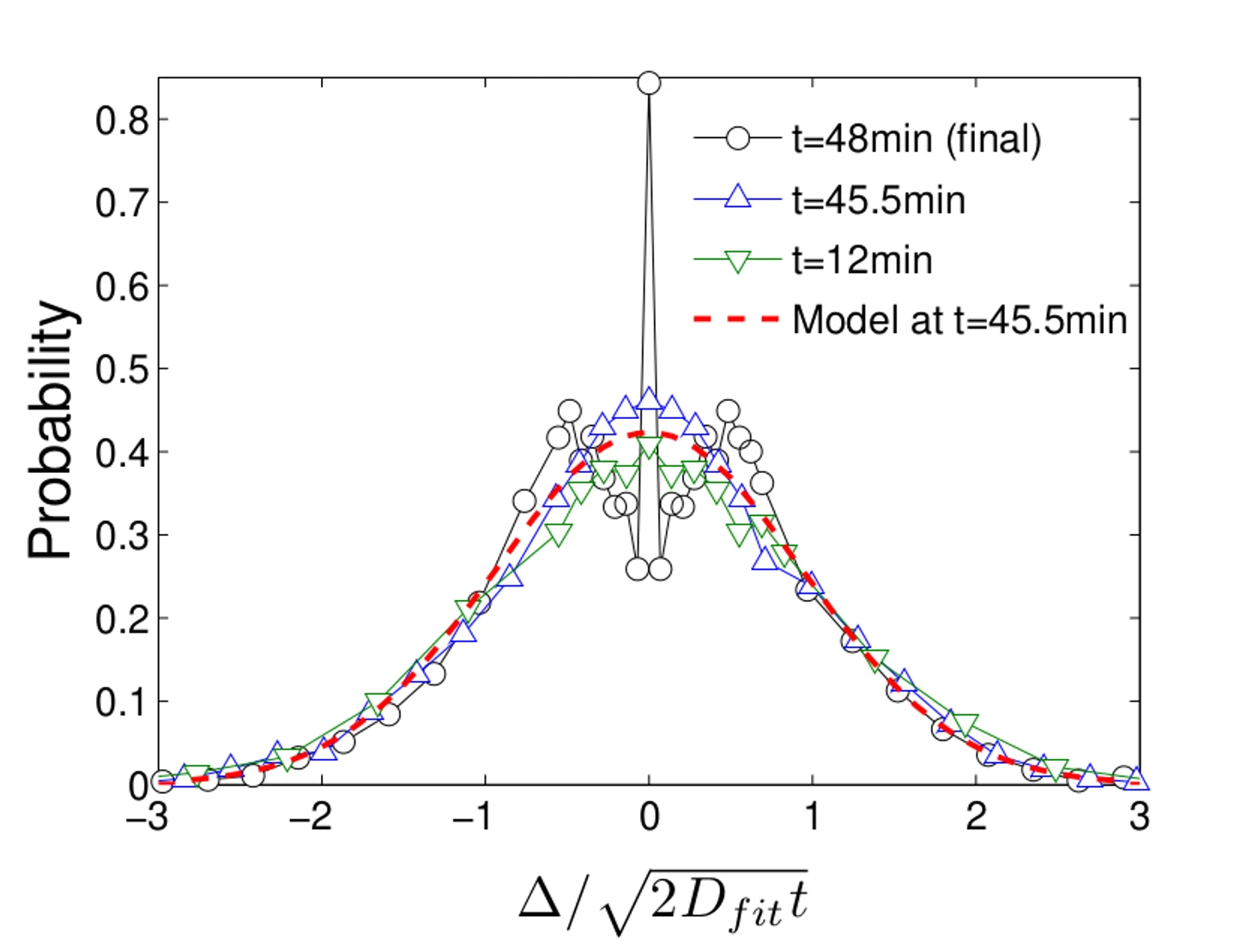
Нормировка нужна для корректного сравнения: разница +20 в конце 4ой четверти гораздо менее удивительна, чем такая же разница уже в конце первой четверти.

Спекуляции

Какие выводы я сделал для себя:

1. Полученная модель хорошо описывает реальные данные за исключением самых последних минут матча и существенно расходится с этими самыми последними минутами. Т.е. Можно сказать, что в баскетболе есть 2 режима

  • Основной – каждая из команд старается найти лучший бросок в нападении и максимально затруднить бросок соперника в защите

  • Клатчевый – ко всему, что есть в основном режиме, добавляется учет времени и необходимой по ситуации стоимости броска

2. Разница во внутренней силе команд мала и при просмотре отдельной игры из-за влияния случайностей сложно судить, какая же команда “внутренне” сильнее 

3. Рывки и голевые засухи, которые в основном происходят в «основном» режиме, можно интерпретировать двояко:

  • Рывок – результат случайности и все замены и перестановки по ходу игры мало влияют на динамику разницы в счете

  • Множество маленьких взаимосвязанных факторов таких, как замены, смещение акцентов в атаке, смена основной защиты, индивидуальные корректировки игроков и т.д., в совокупности дают “случайную” картину  

Фото: Gettyimages.ru/Sarah Stier

logoНБА