xG своими руками
Скорее всего большинству людей узнавших об xG и не считающих эту модель абсурдной / бесполезной так или иначе было интересно узнать, как же получаются эти коэффициенты при ударах. А тех, кто ее таковой считал, я попробую в этом переубедить.
Если говорить формально, то xG - это оператор, переводящий пространство параметров удара в пространство рациональных чисел размерности 2. То есть из параметров удара формируется вектор (например, (50, 70, 30): (x координата, y координата, высота полета мяча)), который затем под воздействием оператора преобразуется в новый вектор (например, (0.3, 0.7): (вероятность гола, вероятность обратного события - не гола)). Простейший пример - матричный оператор:
Получившийся результат: (98, 36) - не совсем подходит, так как нам нужны вероятности. Разделим каждое число на их сумму и получим (0.73, 0.26), где 0.73 и будет вероятностью гола. Не стоит интерпретировать результат - числа в матрице подобраны случайно.
В реальности никто не подбирает коэффициенты для матриц, а рассматривают задачу в контексте машинного обучения. Идея состоит в том, чтобы обучить бинарный классификатор и за показатель xG брать вероятность попадания в первый класс.
Подробнее о технологии
Для своей реализации я выбрал наивный байесовский классификатор, основанный на применении теоремы Байеса. Описание работы классификатора частично взято из статьи, ссылка на которую будет в комментариях
Пусть у нас есть набор параметров, описывающих удар O. Кроме того, имеются классы (в нашем случае целых 2) С, к одному из которых мы должны отнести удар. Нам необходимо найти такой класс с, при котором его вероятность для данного удара была бы максимальна. Математически это записывается так:
Вычислить P(C|O) сложно. Воспользуемся теоремой Байеса и перейдем к косвенным (априорным) вероятностям:
Так как мы ищем максимум от функции, то знаменатель нас не интересует (он в данном случае константа). И теперь запишем удар как набор признаков:
Знаменатель нас не интересует. Но это все еще сложно. Здесь включаем «наивное» предположение о том, что переменные O зависят только от класса C, и не зависят друг от друга. Это сильное упрощение, но зачастую это работает. На самом деле, можно предположить, что признаки удара независимы. Числитель примет вид.
Действительно, намного проще. Финальная формула:
То есть все что нужно сделать, это вычислить вероятности P(C) и P(O|C). Вычисление этих параметров и называется тренировкой классификатора.
Подготовка данных и результаты
Начнем с того, что данные необходимо найти. Как бы парадоксально это не звучало, но найти большое количество хороших данных не тратя безумное количество денег - практически невозможно, поэтому в предыдущих постах (спойлер: и в этом тоже) я часто делал скидку на ограниченность датасета. За основу я взял обезличенный датасет из, примерно, 200 тысяч ударов (да, это очень мало) и сравнивал результат на все тех же открытых данных от StatsBomb по Чемпионату мира. К сожалению, я был немного ограничен и в выборе фич для описания ударов, так как мне нужны были только те, которые, как минимум, присутствуют в обоих датасетах. В итоге для я использовал 4 параметра: 2 координаты, id части тела, которой наносился удар и расстояние от ворот (сейчас особенно внимательные из вас могут справедливо мне предъявить за допущение о независимости признаков).
После обучения модели точность была в районе 70% на тестовых данных первого датасета. Точность считалась по % ударов, в которых модель предугадала исход (> 0.5 - гол), я счел более логичным сравнение байесового xG с xG от StatsBomb. Среднеквадратическая ошибка (MSE) получилась равной 0.0256.
В следующих примерах поле xg - байесовский классификатор, sbxg - xG от StatsBomb:
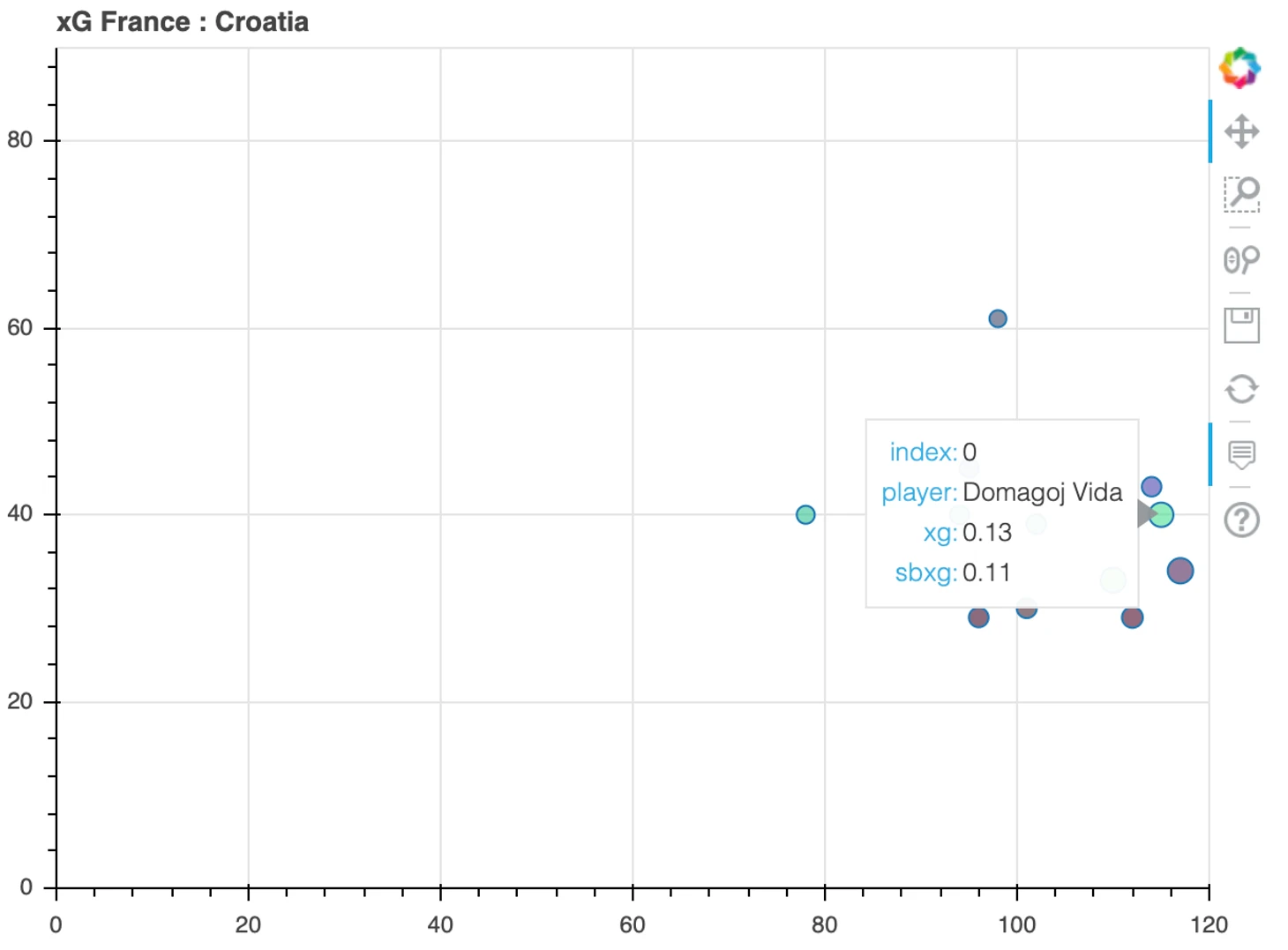
Ссылка на проект в гитхабе и карты по всем матчам ЧМ-2018 в комментариях. Также с радостью отвечу на все вопросы.




Открытые данные StatsBomb: https://statsbomb.com/resource-centre/
Код: https://github.com/dailydaniel/univer/tree/master/xG
Визуализация: https://github.com/dailydaniel/univer/tree/master/xG/code/OUT
Статья понравилась. Подписался, поставил плюс, создавай такого рода контент и дальше)
Да, с формулами беда, буду разбираться как это исправлять. Через браузер на телефоне нормально прогружается.