Как рост и вес влияют на процент выигранных верховых единоборств?
Умение бороться наверху зависит от антропометрических параметров, а также от навыков выбора позиции, координации и тому подобных. Иначе, от факторов, на которые игрок влиять не может, и факторов, которые можно в той или иной степени развивать. Зная антропометрию игроков, можно узнать ожидаемый относительно роста и веса процент выигранных верховых (назовем его xA% - expected aerials percentage).
Процент выигранных верховых единоборств, в отличие от реализации моментов, является относительно повторяемой величиной (R^2 между показателями одного игрока в два последовательных сезона равен 61%), а также не одинаковой для всех игроков на очень длинной дистанции. Поэтому, можно утверждать, что остаток между xA% и А% зависит в первую очередь от мастерства игрока.
В выборку включим всех игроков из топ-5 лиг за сезон 2016/17, вступивших более, чем в 30 верховых единоборств. Таковых оказалось 1 329 человек. Была произведена разбивка на 3 группы: защитники (игравшие на позиции ЦЗ), полузащитники (в том числе фланговые защитники без навыков игры на позиции ЦЗ) и нападающие (без навыков игры на позиции атакующего полузащитника/вингера)
О применимости
В случае отсутствия знаний матстатистики, эту часть можно пропустить почти без вреда для понимания происходящего.
В нашем исследовании будем использовать МНК с коррекцией на гетероскедастичность. Предпосылки о нормальности остатков и независимость остатков друг от друга и независимых переменных более-менее выполняются, однако, очевидно, имеет место некоторая коллинеарность между ростом и весом (R^2 между этими переменными равен 53%). Несмотря на это, считаю, что модель имеет право на существование, так как даже при исправлении мультиколлинеарности результаты не изменятся принципиальным образом, хотя и надежность оценки параметров повысится.
Имелся вариант не учитывать вес игроков, считая его фактором, на который можно влиять. Тогда пропала бы и мультиколлинеарность, но от такой модели было решено отказаться из-за слишком сильного упрощения. Кроме того, стоит понимать, что игроки в разной степени готовы бороться за верховые мячи, поэтому в одних и тех же условиях футболисты могут иметь не одинаковое значение Aerials/90. Но влючать этот показатель в модель как независимую переменную было бы неправильно, поскольку это не фиксированный для игрока параметр. Брать в качестве зависимой число выигранных на 90 минут тоже не кажется оптимальным, поскольку такой показатель не будет учитывать проигранные единоборства.
Можно было бы построить одну общую модель с включением в нее переменных, показывающих позиции игроков, но оказалось, что для защитников, полузащитников и нападающих работают разные закономерности, чтобы объединять их в одну модель. Поэтому будем использовать одинаковые спецификации с разными коэффициентами.
Защитники
Просчитав описанную модель на выборке, состоящей из 407 защитников (средний A% = 59,8%), мы получаем следующее уравнение:
xA% = -35,48 + 0,443 * H + 0,181 * W + LC,
где: Н - рост в самнтиметрах (каждый лишний сантиметр в среднем повышает A% на 0,443%),
W - вес в килограммах (каждый лишний килограмм в среднем повышает А% на 0,181%),
LC - коррекция на лигу, равная 0 для Ла Лиги, -2,94 для Премьер Лиги, 0,13 для Серии А, -3,54 для Бундеслиги и -0,59 для Лиги 1.
Обращает на себя внимание то, что в этом сезоне в Германии и Англии защитники выигрывают верховые почти на реже, чем в других лигах. К слову, именно в этих двух чемпионатах наибольшее число навесов на 90 минут.
R^2 модели равен 16,5%, то есть от мастерства защитника процент выигранных мячей зависит в большей степени, чем от физических данных.
Итак, подставив значения в формулу для всех игроков, получим ожидаемый процент верховых. Отсортировав игроков по разнице между A% и xA%, мы получим список лучших защитников по игре на втором этаже с учетом разных антропометрических параметров:
Заметим, что некоторые игроки из топа имеют малое абсолютное число единоборств. Причины этого могут быть разные. Возможно, процент у таких игроков выровняется на большей дистанции по закону больших чисел, а возможно, дело в манере игры - защитники борются только за те мячи, в которых уверены. Заметим, что это не самое полезное качество для обороняющегося игрока. Тогда защитнику чаще вступать в борьбу - даже если процент ухудшится, число выигранных мячей увеличится, что окажет команде пользу.
Полузащитники
770 полузащитников и вингбэков в выборке (средний A% = 45,1%):
xA% = -91,97 + 0,603 * H + 0,412 * W + LC,
LC: 0 для Ла Лиги, -4,05 для Премьер Лиги, -1,84 для Серии А, -2,93 для Бундеслиги и -2,27 для Лиги 1.
R^2 модели равен 16,6%.
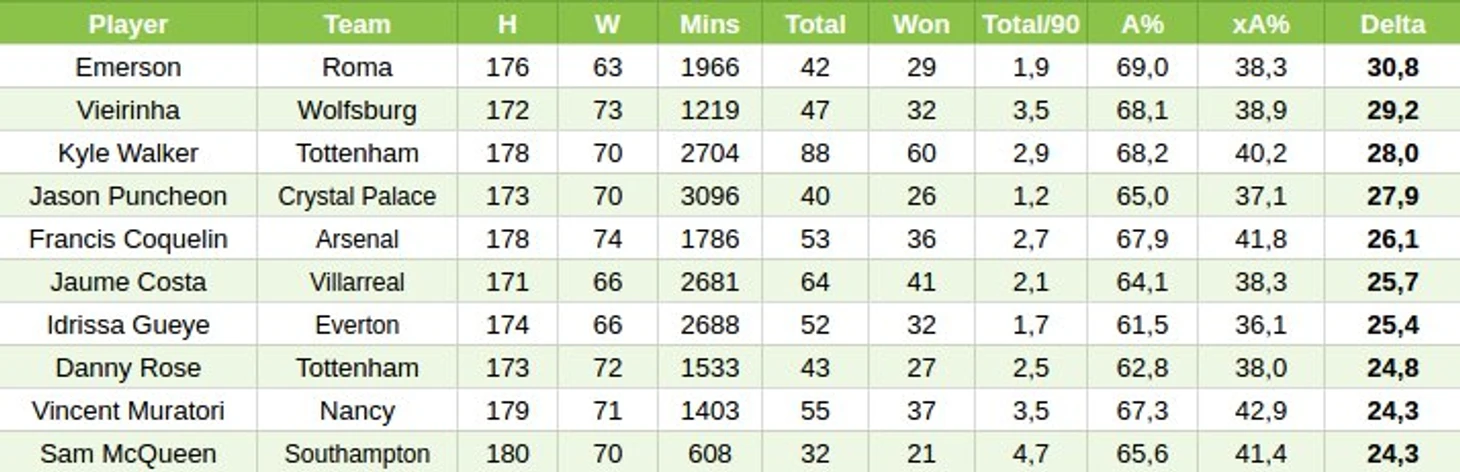
Нападающие
Всего 152 нападающих (средний A% = 41,0%). Так как их оказалось меньше, чем полузащитников и защитников, значимость коэффициентов упала, поэтому откажемся от поправки на лигу.
xA% = -131,96 + 0,750 * H + 0,426 * W
R^2 вырос до 28,6%. Значит, для нападающих рост и вес играют более высокую роль, чем для защитников и полузащитников. Возможно, это связано с тем, что защитники не могут избегать верховой борьбы из-за высокой цены ошибки, а нападающие, не являющиеся столбами, могут относиться к борьбе на втором этаже более халатно.
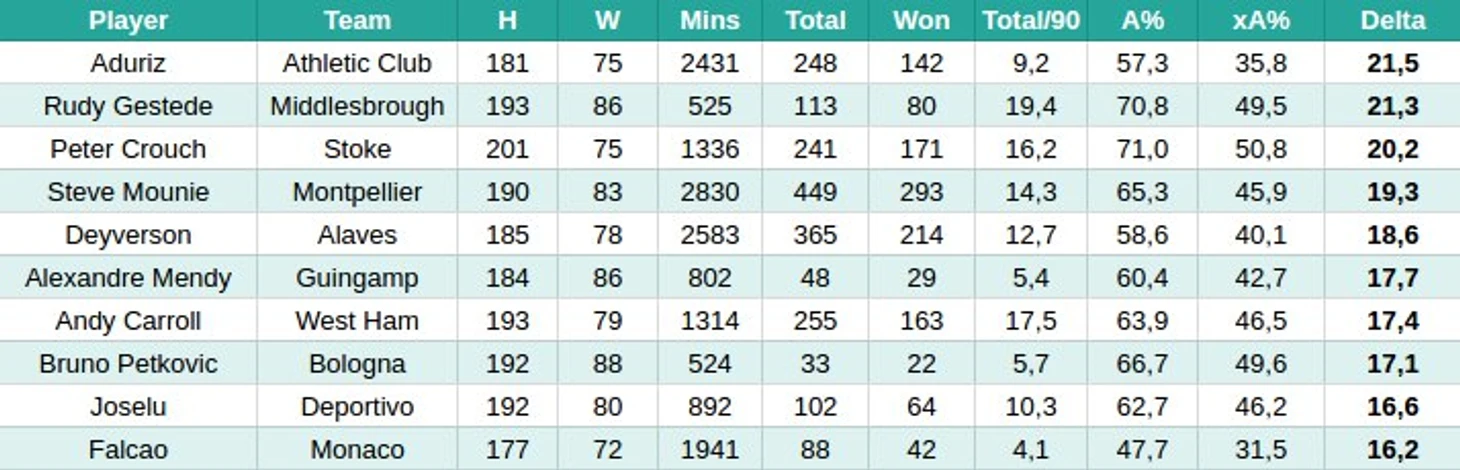
Сразу два форварда сборной Бенина (Жестед и Муни) имеют выдающиеся цифры как по проценту выигранных, так и по абсолютному числу верховых на 90 минут.
Заключение
Безусловно, модель можно улучшать, используя иные спецификации и добавляя новые переменные, но и в таком базовом варианте мы получили интересные результаты. Даже в нынешнем виде показатель A% - xA% может использоваться для оценки именно умения игрока вести борьбу за верховые мячи, очищенного от влияния габаритов.
Идея материала была подана Никитой Васюхиным.
Больше аналитики в Блокноте.
А как ты высчитывал коэффициент отклонения по росту в лигах? Учитывал ли ты средний рост лиги и коэффициент отклонения роста игрока от ср. роста по лиге?
Для расчетов коэффициентов использовался МНК, скорректированный на гетероскедастичность, о чем было сказано в пункте про применимость.